Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Розрахунок гвинтової циліндричної пружини з малим кроком.
|
|
Розглянемо пружину (рис.10.7а) під дією зовнішнього навантаження F. Основні параметри (рис.10.7б): D1 – внутрішній діаметр пружини (діаметр утворюючої циліндра, діаметр оправки); D – середній (розрахунковий) діаметр; D2 – зовнішній діаметр; d – діаметр прутка; a – кут нахилу витка.
Приведемо зовнішню силу F до центра ваги поперечного переріза витка. Зневажаючи через малість поздовжньою силою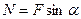 
і згинальним моментом 
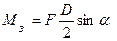, одержимо (рис.10.7в) поперечну силу Q = F і крутильний момент 
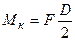. Від дії поперечної сили Q (деформація зсуву, зрізу) у перерізі виникають дотичні напруження tз, що умовно приймемо рівномірно розподіленими по перерізу (рис.10.7г) і рівними: 
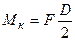. Від дії крутильного моменту також виникають дотичні напруження, що лінійно розподіляються по перерізу (рис.10.6д) і мають максимальне значення tкmax у крайніх точках перерізу: 
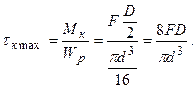З епюр, приведених на рис..10.7г та 10.7д видно, що дотичні напруження tз і tк в т. А збігаються по напрямку.
Рис.10.7.
Підсумуемо дві епюри (рис.10.7г і рис.10.7д) і одержимо, що в пружині найбільш навантажені внутрішні точки (точка А), а максимальні напруження:
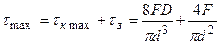
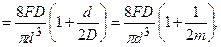(10.17) де 
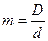– індекс пружини. При розрахунку пружин великого діаметра D з тонкого дроту (
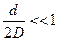) максимальні напруження з достатнім ступенем точності можна визначити за формулою: 
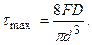З урахуванням напружень від поздовжньої сили, згинального моменту та поперечної сили остання формула прийме вигляд:
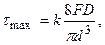(10.18)
де поправочний коефіцієнт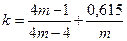 
, значення якого в залежності від індексу пружини m приведені нижче:
| ||||||||
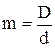
| k | 1, 58 | 1, 4 | 1, 31 | 1, 25 | 1, 21 | 1, 18 | 1, 16 | 1, 14 |
При визначенні осадки l (деформації) гвинтової циліндричної пружини врахуємо лише деформацію від кручення. Деформаціями зсуву, розтягання-стискання та згинання зневажають через їхню малість.
Потенційна енергія деформації пружини при статичному навантаженні чисельно дорівнює роботі зовнішньої сили F на відповідному переміщенні l, тобто:
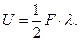(10.19)
Обчислимо потенційну енергію деформації при крученні витків пружини, для чого виріжемо нескінченно малий елемент довжиною ds (рис.10.8). Жорстко закріпимо один його кінець, на вільному кінці стержня прикладемо виникаючий крутильний момент .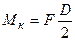
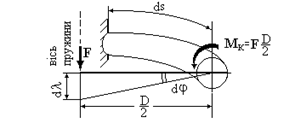
Рис.10.8.
Вільний крайній переріз елементарного стержня повернеться на кут dj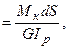 
а точка прикладення сили F одержить переміщення dl. Вважаючи незначним вплив кривизни елементарного стержня, величину потенційної енергії при крученні одного витка пружини стержня обчислимо за формулою (10.15) 
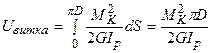. З огляду на те, що крутильний момент 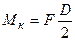, полярний момент інерції 
, пружина має n витків, потенційна енергія при статичному навантаженні пружини силою F дорівнює:
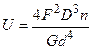. (10.20)
Порівнюючи значення потенційної енергії, що обчислюється за формулою (10.19) і (10.20), залежність для визначення осадки l прийме вигляд:
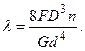(10.21)
Щоб пружина була більш податливою, діаметр прутка повинний бути найменшим, при цьому максимальні дотичні напруження досягають значних величин. Для виключення цієї невідповідності пружини виготовляються зі спеціальних пружинних матеріалів, що мають високі міцні характеристики. Приведемо значення допустимих дотичних напружень для пружинних матеріалів: високо загартовані пружинні сталі: [t] =500 МПапри діаметрі прутка d = 6 мм; [t] = 400МПа при d = 10 мм; [t] = 380 МПа при d = 12 мм; хромонікелеві сталі: [t] = 700 МПа при d = 12 мм; фосфористі бронзи: [t] = 130 МПа при d = 16 мм.
КОНТРОЛЬНІ ПИТАННЯ
1. В якому випадку виникає кручення?
2. Яка існує залежність між крутильним моментом, потужністю, що передається валом, і числом обертів?
3. Які припущення лежать в основі теорії кручення стрижнів круглого перетину?
4. Який кут називається відносним, повним кутом закручування?
5. Як записуються формули для відносного і повного кутів закручування?
6. Що називається полярним моментом інерції і яка його розмірність?
7. Напишіть формулу полярного моменту інерції для суцільного круглого і кільцевого перетинів.
8. Що називається жорсткістю при крученні?
9. В яких точках перетину валу виникають найбільші напруження при крученні?
10. Як розподіляються напруження кручення по поперечному перетині валу?
11. В чим полягає перевага валу кільцевого перетину в порівнянні з валом круглого перетину?
12. Напишіть формулу для визначення дотичних напружень в будь-якій точці поперечного перетину валу круглого перетину.
13. Напишіть умову міцності при крученні.
14. Що називається моментом опору крученню? Яка його розмірність?
15. По яких формулах визначаються полярні моменти опору крученню стрижня суцільного і кільцевого перетинів?
16. Як повинен змінитися діаметр валу, якщо потужність, що передається ним, залишається без зміни, а число обертів збільшується?
17. В яких точках перетину виникають найбільші дотичні напруженні при крученні бруса прямокутного поперечного перетину?
18. Як виражається потенційна енергія деформації при крученні?
19. Які напруженні виникають у витках циліндрової гвинтової пружини при її розтяганні-стисканні?
20. З яких міркувань і по якій формулі визначається осідання гвинтової циліндрової пружини?
Лекція № 11. Стійкість стиснутих стрижнів.Вступ.
1. Вступ.
При розрахунках на міцність і жорсткість вважалося, що під час деформації будь-якої системи має місце лише одна наперед відома форма рівноваги. Насправді рівновага у деформованому стані між зовнішніми та внутрішніми силами пружності може бути не тільки стійкою, а й нестійкою.
Пружна рівновага буде стійкою, якщо деформоване тіло при будь-якому малому відхиленні від стану рівноваги намагається повернутися до початкового стану й повертається до нього після припинення зовнішнього впливу.
Пружна рівновага нестійка, якщо деформоване тіло, виведене неї будь-якою зовнішньою дією, продовжує деформуватися в напрямі наданого йому відхилення.
Навантаження, перевищення якого спричиняє втрату стійкості вихідної форми тіла, називають критичним і позначають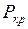 
. Можна стверджувати, що досягнення навантаженнями критичних значень рівнозначно руйнуванню конструкції, оскільки нестійка форма рівноваги неминуче буде втрачена, що пов¢ язано з практично необмеженим зростанням деформацій та напружень.
До моменту настання критичного стану пружні деформації за модулем зовсім невеликі, і зростання їх майже непомітне для ока. Проте з моменту настання критичного стану до моменту руйнування залишкові деформації наростають надто швидко і практично немає часу вжити заходів щодо запобігання катастрофи, яка загрожує.
Для забезпечення певного запасу стійкості необхідно, щоб задовольнялася умова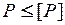 
. Тут 
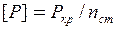, де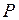 
- діюче навантаження, 
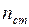- коефіцієнт запасу стійкості.
Отже для розрахунків стиснутих стрижнів на стійкість необхідно знати засоби визначення критичних навантажень.
2. Формула Ейлера для визначення критичної сили стиснутого стрижня.
|
 |
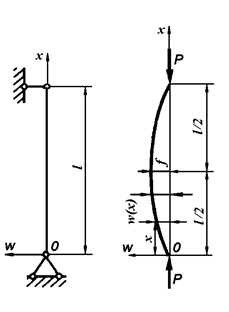Розглянемо стрижень з шарнірно закріпленими кінцями (рис.11.1а), який трохи зігнувся під дією сили 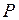, яка дещо перевищує критичну силу 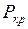. Віднесемо викривлену вісь стрижня до прямокутної системи координат 
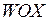(рис. 11.1б) і припустимо, що напруження в стрижні під дією сили 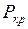не перевищують границю пропорційності. Для визначення поздовжньої сили скористаємось наближеним диференційним рівнянням пружної лінії:
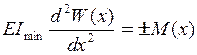, (11.1)
де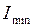 
- найменший момент інерції перерізу стрижня. Оскільки 
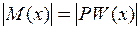, а знак прогину завжди протилежний знаку другої похідної, тобто знаки 
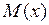і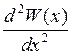 
протилежні при будь-якому напрямі 
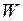, то в правій частині (11.1) треба ставити знак „мінус”. Тоді рівняння (11.1) набуває вигляду
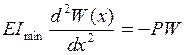, або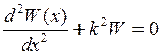 
, (11.2)
де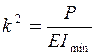 
.(11.3)
Ми отримали однорідне лінійне диференціальне рівняння другого порядку, загальний інтеграл якого можна представити у вигляді:
.
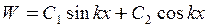Сталі інтегрування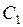 
і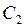 
визначаємо з граничних умов 
, 
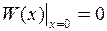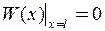. З першої граничної умови випливає, що 
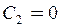, а з другої знаходимо 
.
При викривленій формі стрижня має виконуватися рівність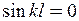 
. Корінь цього рівняння 
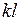може мати нескінчену кількість значень: 
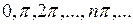, тобто
,
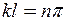де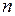 
- довільне ціле число.
Однак перший корінь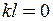 
відкидається, оскільки він не відповідає вихідним даним задачі. Отже, 
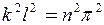, тоді з рівняння (11.3) дістанемо вираз для сили, що стискає:
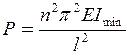.(11.4)
Рівняння (11.4) має назву формули Л.Ейлера.
Практично нас цікавить найменше значення поздовжньої сили 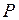, при якому стає можливим поздовжнє згинання. Найменше значення критичної сили 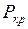визначимо при 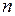=1 та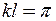 
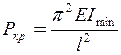(11.5)
3. Вплив умов закріплення кінців стрижня на значення критичної сили.
Розглянемо інші приклади закріплення кінців стрижня.
1) Стрижень завдовжки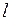 
закріплений одним кінцем та стиснутий поздовжньою силою, прикладеною до вільного кінця (рис. 11.2а).
|
|
|
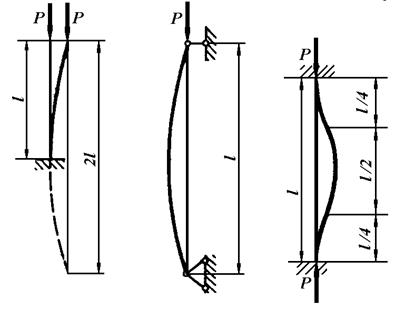
Якщо порівняти рис. 11.2а з рис. 11.2б, бачимо, що зігнута вісь стрижня, закріпленого одним кінцем, перебуває в тих самих умовах, що й верхня половина стрижня завдовжки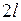 
з шарнірно закріпленими кінцями.
Отже, критична сила для стрижня з одним закріпленим кінцем дорівнює
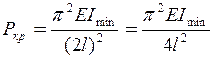.(11.6)
2) Стрижень завдовжки 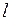, обидва кінця якого жорстко закріплені (рис. 11.3).
Після втрати стійкості стрижня внаслідок його симетрії його середня частина завдовжки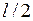 
працює в тих самих умовах, що й стрижень при шарнірно опертих кінцях. Критичну силу в цьому разі знаходимо з рівняння (11.4), якщо в ньому замість 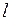покласти 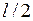, що дає
.(11.7)
3) Стрижень завдовжки 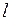, жорстко закріплений одним кінцем та пружно опертий на іншому (рис. 11.4).
|
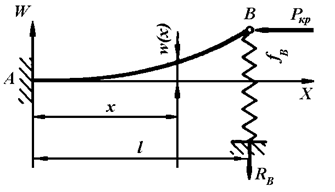
Рис. 11.4.
Після втрати стійкості опертий кінець стрижня переміщується у вертикальному напрямі на величину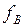 
, 
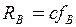, де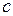 
- коефіцієнт пружності опори В.
Складемо диференційне рівняння пружної ліній стиснутого стрижня після втрати стійкості
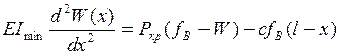
Поділивши кожний член рівняння на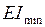 
та позначивши 
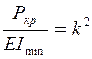, отримаємо
.
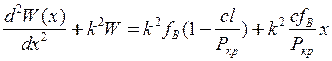Загальний інтеграл цього рівняння
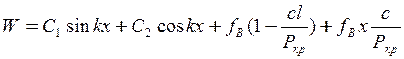.(11.8)
Для визначення сталих інтегрування 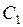і 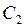і критичного навантаження маємо такі граничні умови:
при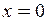 
, 
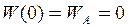при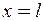 
.
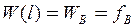Використовуючи граничні умови при 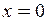знаходимо стал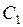і і :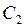
; 
.
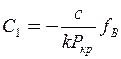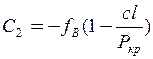Підставивши у (11.8) замість довільних сталих отримані вирази, запишемо остаточно рівняння зігнутої осі стиснутого стрижня
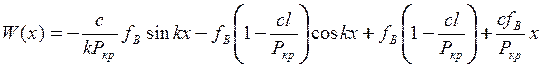.(11.9)
Щоб вивести рівняння, яке дає можливість визначити критичне навантаження, використовуємо граничну умову при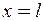
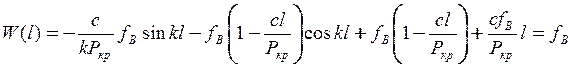, або
,
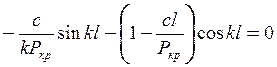звідки з урахуванням (11.3) маємо
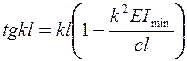.(11.10)
Якщо розв’язати це рівняння, тобто визначити найменший корінь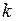 
(
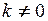), то тим самим можна знайти значення критичного навантаження, оскільки 
.
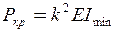Розглянемо два граничних випадки.
При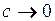 
маємо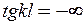 
, тобто 
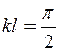і таку розрахункову схему стрижня, коли один кінець (лівий) жорстко закріплений, а інший (правий) вільний. Критична сила
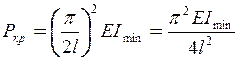
збігається з виразом (11.6).
При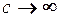 
(дуже жорстка опора – защемлення) запишемо визначальне рівняння
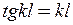, тобто 
.
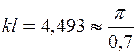Критична сила
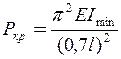, (11.11)
що дає формулу для стрижня, один кінець якого закріплений, а інший шарнірно опертий.
Співвідношення (11.5), (11.6), (11.7), (11.11) можна об’єднати в одну формулу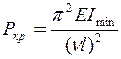 
, (11.12)
де 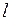- фактична довжина стрижня, 
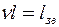- зведена довжина стрижня, 
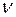- коефіцієнт зведення довжини. Отже різні випадки обпирання та навантаження стрижня зводяться до основного випадку введенням у формулу для 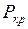так званої зведеної довжини. Це поняття вперше було використано Ф.С.Ясинським. З формули Ейлера (11.12) випливає, що критичне навантаження залежить від найменшої жорсткості 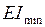, довжини стрижня 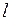та коефіцієнта 
.
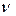Так, якщо коефіцієнт пружності опори 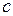змінюється від 0 до 
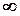, то це можна врахувати коефіцієнтом зведення 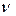, який при цьому відповідно змінюється від 2 до 0, 7 (див. рис.11.5).
|
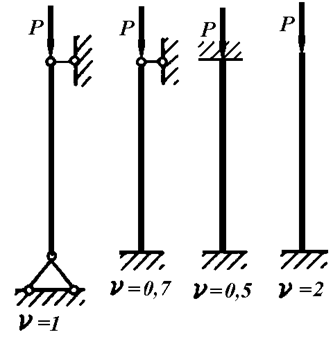
Рис.11.5.
Треба підкреслити, що виведення формули (11.12) ґрунтується на застосуванні диференціального рівняння рівної пружної лінії. Тому використовувати цю формулу можна лише тоді, коли справедливий закон Гука, тобто доки критичне напруження (напруження стискання, що відповідає критичній силі) не перевищує границі пропорційності:
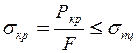, де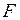 
- площа перерізу стрижня.
Розглянемо чисельний приклад: визначити 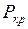для круглого стрижня діаметром 
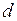=0, 05 м, довжиною 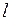=2 м (рис. 11.4). Матеріал стрижня Ст3, модуль пружності 
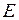=2, 1× 105 МПа, границя пропорційності 
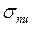= 200 МПа, коефіцієнт пружності опори 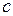=7000 Н/м.
Розв’язок:
Момент інерції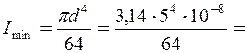 
30, 66× 10-8 м4. Запишемо рівняння (11.10) у вигляді 
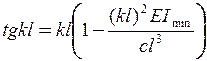. Покладемо 
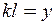і, підставивши чисельні значення відомих величин, отримаємо трансцендентне рівняння
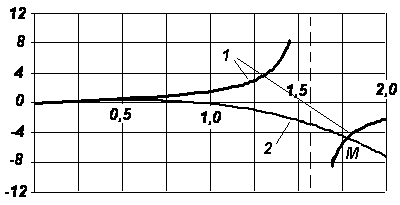
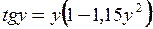, яке не має аналітичного розв’язку. Серед нескінченої кількості його коренів нас цікавить найменший ненульовий. З геометричної точки зору це є абсциса точки 
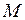перетину гілки функції 
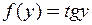(рис. 11.6, крива 1), 
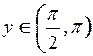з дугою кубічної параболи 
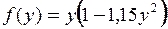(рис. 11.6, крива 2).
Введемо функцію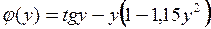 
.
При 
маємо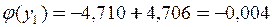 
,
при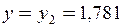 
маємо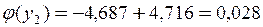 
.
Остаточно приймаємо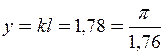 
, що дає можливість визначити критичну силу 
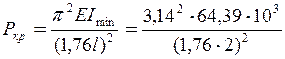=51, 24 кН.
Відповідно до неї критичне напруження становить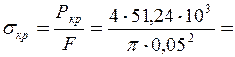 
26, 1 МПа < 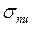=200 МПа.
|
Отже, критичне напруження менше границі пропорційності, а це в свою чергу означає правильність розрахунку критичної сили.
КОНТРОЛЬНІ ПИТАННЯ
1. В чим полягає суть явища подовжнього вигину?
2. Які види рівноваги називаються СТІЙКИМ, НЕСТІЙКИМ, БАЙДУЖИМ?
3. Яке навантаження називається критичним?
4. Що називається запасом стійкості?
5. Як в загальному вигляді записується формула ЕЙЛЕРА?
6. Що називається коефіцієнтом приведення довжини і чому він дорівнює для чотирьох випадків закріплення кінців стрижня?
7. Чи можливі проміжні випадки?
8. Який момент інерції перетину підставляється у формулу ЕЙЛЕРА? Чому?
9. В якому випадку вірогідність витріщення стрижня на всіх напрямках однакова?
10. Що називається гнучкістю стрижня? Яка її формула?
11. Для яких випадків застосовується формула ЕЙЛЕРА?
12. Як записується формула для визначення критичних напружень при втраті стійкості за межею пружності?
13. Що визначає собою коефіцієнт при визначенні напруженні стискання, що допускається?
14. Від чого залежить коефіцієнт?