
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Спектр амплитудно-модулированного колебания
|
|
Пусть задано высокочастотное модулированное колебание, о котором известно, что частота w0 и начальная фаза q0величины постоянные, а огибающая A(t) содержит в себе передаваемое сообщение s(t). Аналитически такое колебание можно представить с помощью SAM(t)= = A(t)cos( w0 t +q0). Требуется установить связь между спектром модулированного колебания и спектром модулирующей функции, т. е. спектром исходного, сообщения s(t). Проще и нагляднее всего это можно сделать для тональной (гармонической) модуляции, когда огибающая A (t) = A 0 [1+ M cos(W t +g)]
а модулированное колебание определяется выражением a (t) = A0 [ 1+ M cos(W t +g) ] cos(w0 t +q0). Перепишем это выражение в виде a (t) = A0 [ cos(w0 t +q0) + M cos(W t +g) cos(w0 t +q0) ],
где второе слагаемое в правой части этого выражения, являющееся продуктом модуляции, можно привести к виду:
M cos (W t +g) cos(w0 t +q0) =M/2cos[ω 0 +W)t+(q+g)]+M/2cos[ω 0-W)t+(q-g)]
после чего развернутое выражение колебания a(t) принимает вид:
a(t) = A0cos (w0 t +q0)+ M/2cos[ω 0 +W)t+(q+g)]+M/2cos[ω 0-W)t+(q-g)]
Первое слагаемое в правой части представляет собой исходное немодулированное колебание с частотой w0. Второе и третье слагаемые соответствуют новым колебаниям гармоническим), появляющимся в процессе модуляции амплитуды. Частоты этих колебаний ω 0 +W и
ω 0 - W называются верхней и нижней боковыми частотами модуляции. Амплитуды этих двух колебаний одинаковы и составляют от амплитуды немодулированного колебания долю, равную М/2, а их фазы симметричны относительно фазы несущего колебания.
Картину образования спектра амплитудно-модулированного колебания проще всего пояснить на примере, когда модулирующее сообщение s(t) является суммой колебаний нескольких колебаний. Допустим, что исходное низкочастотное сообщение представляет собой сумму гармонических сигналов: тогда общее аналитическое выражение для напряжения равно:
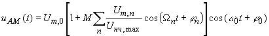
В этой формуле Um, 0 – амплитуда несущего колебания; Um, n – амплитуды
модулирующих сигналов. Качественный спектр такого АМ-колебания при n=2 имеет вид, показанный на рис. 1
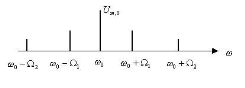
Рис.1