
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вопрос 14 Параметры случайных сигналов
|
|
Наибольшее значение имеют следующие характеристики случайного
процесса:
· математическое ожидание или первый начальный момент, равный
µ
Mx(t)=M[x(t)]= ò xp(x; t)dx
-µ
Математическое ожидание – это средняя функция, вокруг которой группируются реализации (см.рис. 1).
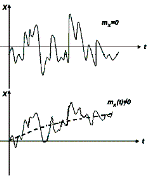
Рис. 1
Многие параметры случайного процесса получают путем вычисления простейших функций от математического ожидания.
· дисперсия (разброс реализаций случайной величины относительно математического ожидания)
Dx(t)= M{[x(t) -mx(t)]2}
Корень квадратный от дисперсии называют среднеквадратическим отклонением (СКО):
sÖ M{[x(t)- mx(t)]2}=Ö Dx(t)
Если сечения случайного процесса описываются одним и тем же законом распределения, то математическое ожидание и дисперсия являются числами (параметрами). Если mx=0, то говорят, что такой процесс имеет нулевое среднее; процесс x(t)- mx (t) называется центрированным. Математическое ожидание называют первым моментом случайной величины, дисперсию – вторым центральным моментом.
Если для случайного процесса заданы двумерные плотности вероятно-
сти, что бывает необходимо при анализе быстроменяющихся процессов, то
определяют так называемую ковариационную функцию
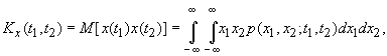
которая определяет математическое ожидание произведений случайных функций в моменты t1 и t2. При t1= t2 имеем
µ
Kx(t1, t2)= ò X12 p(x1; t1)dx1=M[x2(t)]
-µ
т. е. при нулевом интервале между t1, t2 ковариационная функция определяет математическое ожидание от квадрата случайной величины. Разность между случайной величиной и её математическим ожиданием определяет флуктуации (изменения) сигнала. Для описания флуктуаций определяется автокорреляционная функция процесса
Rx (t1, t2)=M{[x(t1)-mx(t1) ][ x(t2)-mx(t2) ]} =Kx(t1, t2) - mx(t1) mx(t2)
При t1= t2 получаем
Kx(t1, t2)-mx2(t)=Rx(t1, t2)=Dx(t)
т.е. автокорреляционная функция в этом случае равна дисперсии. Часто при-
меняют нормированную корреляционную функцию
rx(t)= Rx(t)/Dx=[Kx(t)-(x)2]/Dx
Все эти функции: Kx(t), rx(t), Rx(t) – характеризуют связь между значениями случайного процесса, разделенными промежутком времени t. Чем медленнее меняется случайная функция, тем больше t, в пределах которого эти функции не равны нулю, т. е. наблюдается статистическая связь между ними.