
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Понятие комплексной частоты.
|
|
Спектральные методы основаны на том, что исследуемый сигнал представляется в виде суммы неограниченно большого числа элементарных слагаемых, каждое из которых периодически изменяется во времени по закону exp (jω t).
Естественное обобщение этого принципа заключено в том, что вместо комплексных экспоненциальных сигналов с чисто мнимыми показателями вводят в рассмотрение экспоненциальные сигналы вида exp (pt), где p— комплексное число: p=σ +jω получившее название комплексной частоты.
Из двух таких комплексных сигналов можно составить вещественный сигнал, например, по следующему правилу:
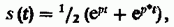
Где p*= σ - jω — комплексно-сопряженная величина.
Действительно, при этом
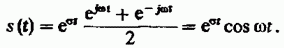
В зависимости от выбора вещественной и мнимой частей комплексной частоты можно получить разнообразные вещественные сигналы. Так, если σ =0, но ω ≠ 0 получаются обычные гармонические колебания вида cos ω t. Если же ω =0 то в зависимости от знака σ получаются либо нарастающие, либо убывающие во времени экспоненциальные колебания. Более сложную форму такие сигналы приобретают, когда ω ≠ 0. Здесь множитель exp (σ t) описывает огибающую, которая экспоненциально изменяется во времени. Некоторые типичные сигналы изображены на рис. 2.10.
Понятие комплексной частоты оказывается весьма полезным прежде всего потому, что это дает - возможность, не прибегая к обобщенным функциям, получать спектральные представления сигналов, математические модели которых неинтегрируемы.
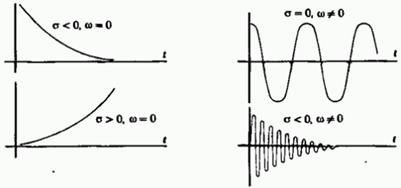
Рис. 2.10. Вещественные сигналы, отвечающие различным значениям комплексной частоты