Вопрос № 2 Периодические сигналы. Ряд Фурье. АЧХ и ФЧХ спектра различные.

Периодическим сигналом (током или напряжением) называют такой вид воздействия, когда форма сигнала повторяется через некоторый интервал времени T, который называется периодом. Простейшей формой периодического сигнала является гармонический сигнал или синусоида, которая характеризуется амплитудой, периодом и начальной фазой. Все остальные сигналы будут негармоническими или несинусоидальными. Существует общая методика исследования периодических негармонических сигналов (входных воздействий и их реакций) в электрической цепи, которая основана на разложении сигналов в ряд Фурье. Данная методика состоит в том, что всегда можно подобрать ряд гармонических (т.е. синусоидальных) сигналов с такими амплитудами, частотами и начальными фазами, алгебраическая сумма ординат которых в любой момент времени равна ординате исследуемого несинусоидального сигнала. Амплитудно - частотная (АЧХ) и фазо -частотная (ФЧХ) характеристики

Частотная характеристика 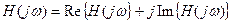представляет собой комплексную функцию действительной переменной – частоты ω. Она может быть записана в виде модуля и аргумента

.

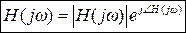Модуль 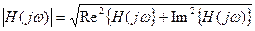- это амплитудно – частотная характеристика (magnitude response) или АЧХ системы. АЧХ означает зависимость модуля ЧХ системы от частоты.

Аргумент 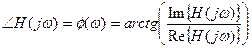- фазо- частотная характеристика (phase response), ФЧХ системы или просто фазовая характеристика системы.

Из выражения анализа системы в частотной области 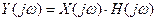следует

,

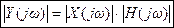т.е. модуль каждой частотной составляющей выхода равен модулю входа, умноженному на значение АЧХ системы на рассматриваемой частоте ω.

Фаза частотной составляющей выхода

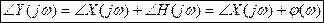
сдвинута относительно фазы входа 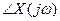на значение ФЧХ системы на данной частоте .

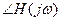Ранее при рассмотрении свойств преобразования Фурье (НВПФ) было показано, что для действительной функции модуль преобразования Фурье – четная функция, аргумент - нечетная функция частоты ω. Поэтому АЧХ реальной системы с действительной импульсной характеристикой h(t) – четная функция ω, ФЧХ – нечетная функция частоты, т.е.

.

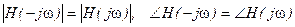В связи с этим на графиках часто изображают АЧХ и ФЧХ только для положительных значений частот.