
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вопрос 3 Непериодические сигналы
|
|
В теории спектрального представления непериодических (импульсных) сигналов используют искусственный прием, позволяющий формально заменить такие сигналы периодическими с бесконечно большим интервалом (периодом) следования, т. е. при Т → ∞. Предположим, что имеется одиночный импульсный сигнал s(t) конечной длительности и произвольной формы. Дополним его такими же сигналами, периодически следующими через некоторые интервалы времени – Т (рис. 1). В результате получим периодическую последовательность sпер(t), которую можно представить в виде ряда Фурье (1.7).
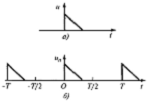
Рис. 1. К определению непериодических сигналов:
а - один импульс; б - условное периодическое представление
Для перехода к одиночному импульсу увеличим до бесконечности период повторения импульсов – Т. В этом случае в спектральной области произойдут следующие изменения:
· частоты n w0 и (n +1)w0 окажутся сколь угодно близкими и поэтому дискретную переменную n w0 можно заменить непрерывной – w, то есть текущей частотой;
· амплитудные коэффициенты c n станут бесконечно малыми (стремящимися к нулю) из-за наличия Т→ ∞ в знаменателе коэффициентов ряда;
При увеличении периода следования импульсов линейчатый спектр будет все более плотным. В предельном случае, когда период T → ∞, равные расстояния между спектральными линиями уменьшаться настолько, что спектр станет сплошным, а амплитуды отдельных спектральных составляющих окажутся бесконечно малыми. При этом частота следования импульсов ω 0 = 2 π / Т → 0 и превращается в d ω, дискретная переменная n ω 1 – в мгновенную (текущую) частоту ω, а знак суммы трансформируется в интеграл. Pассмотрев интервал частот ∆ w→ 0 в окрестностях некоторой частоты w0, то в пределах этого интервала будет содержаться N отдельных пар спектральных составляющих, частоты которых будут отличаться друг от друга сколь угодно мало (N=∆ w/w0=∆ wT/2π). В результате отмеченных преобразований спектральные составляющие можно суммировать так, как если они имеют одну и ту же частоту и характеризуются одинаковыми комплексными амплитудами. Комплексная амплитуда эквивалентного гармонического сигнала внутри интервала Dw будет равна:
∞ ∞
∆ Aw0 =2N/T ò s(t)ejw0tdt=∆ w/π ò s(t)ejw0tdt
-∞ - ∞
При этом обозначим функцией интеграл:
S(jw)= ò s(t)ejw0tdt
который называется спектральной плотностью сигнала s(t) или прямым преобразованием Фурье данного сигнала.
Спектральная плотность характеризует интенсивность сплошного распределения амплитуд гармоник непериодического сигнала вдоль оси частот w. Это основное отличие спектральной плотности непериодического сигнала от дискретного спектра периодического сигнала, в котором каждая гармоническая составляющая имеет вполне определенное значение частоты и отстоит от соседней на величину ω 0= 2π /Т. Дискретный спектр периодического и спектральная плотность непериодического сигналов имеют разные размерности. Дискретный спектр периодического напряжения или тока имеет размерность амплитуды (В или А). Спектральная плотность имеет размерность В/Гц или А/Гц. Спектральная плотность S(w0)=S(2π f0) – масштабный множитель, связывающий малую длину интервала частот ∆ f и отвечающую ему комплексную амплитуду ∆ A гармонического сигнала на центральной частоте f0. При решении обратной задачи, то есть при нахождении сигнала по его спектральной плотности, необходимо воспользоваться обратным преобразованием Фурье для сигнала s(t):
¥
s(t)= ò S(jw) ejw0tdt
-¥
Основное условие существования спектральной плотности сигнала: для того, чтобы сигналу s(t) можно было бы сопоставить его спектральную плотность S(jw), необходимо, чтобы сигнал был абсолютно интегрируем, то есть, чтобы существовал интеграл:
¥
ò | s (t) | dt < +¥.
-¥
Этот интеграл определяет условие существования спектральной плотности сигнала. В математике детально исследован вопрос о том, какими свойствами должна обладать функция s(t) для того, чтобы ее преобразование Фурье действительно существовало. Так, в указанном классическом смысле невозможно говорить о спектральной плотности гармонического сигнала и(t) =Umсоsw0 t, существующего на всей бесконечной оси времени. В современной математике разработаны приемы, позволяющие разумным образом вычислять спектральные плотности так называемых «неинтегрируемых» сигналов. Такие спектральные плотности будут уже не обычными, классическими, а обобщенными функциями.
|S(w)|=√ [A(w)]2 +[B(w)]2 – амплитудно-частотная характеристика (АЧХ);
q(w)= - arctg [B(w)/A(w)] – фазо-частотная характеристика (ФЧХ).