Интегрирование тригонометрических выражений

1) Интеграл вида

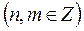
а) Если n - четное число и m - четное, то подынтегральное выражение преобразуют с помощью формул:

,

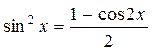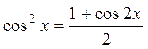
б) Если одно из чисел m или n – нечетное, то выполняют замену:

t = sin x, если n – нечетное;

t = cos x, если m – нечетное.

Эта замена приводит к интегрированию степенных интегралов или рациональных дроби.

в) Если оба числа m и n – нечетные, то интеграл берется как в случае замены:

t = sin x, так и t = cos x.

Пример 25.

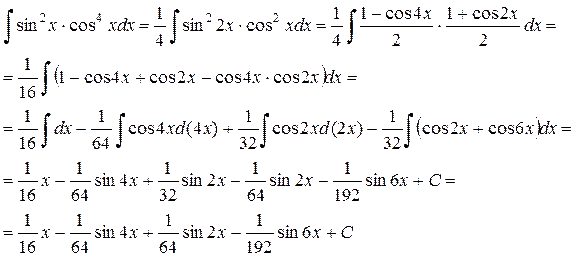
Ответ: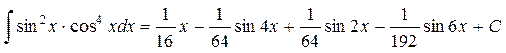

Пример 26.

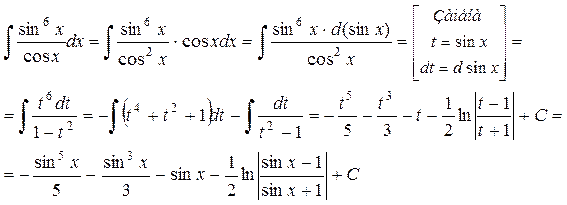
Ответ: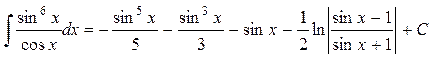

Пример 27.

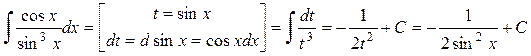
Ответ: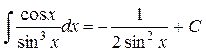

2) Интегралы вида:

; ; .

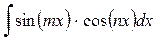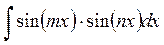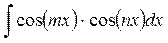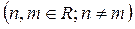
Такие интегралы находят после предварительного применения формул:

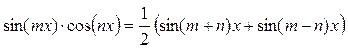
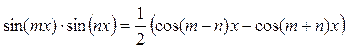
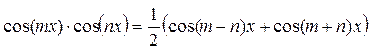
Пример 28.

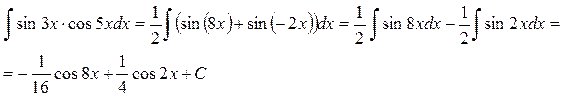
Ответ: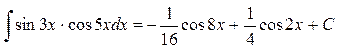

3) Интегралы вида 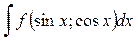, где f (u; V) – рациональная функция двух переменных.

Такие интегралы приводятся к интегралам от рациональных дробей с помощью замены:

;

;

;
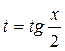
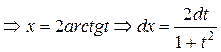
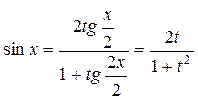