Интеграл с переменным верхним и постоянным нижним пределами и его свойства

Определение 4. Пусть функция y = f (x) непрерывна на [ a; b ]. Тогда она непрерывна на [ a; x ] для любого xÎ [ a; b ]. Следовательно, на [ a; b ] определена функция 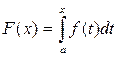, которая называется интегралом с переменным верхним пределом.

Свойства этой функции сформулируем в виде теоремы.

Теорема 3. Пусть функция f (x) непрерывна на [ a; b ]. Тогда функция 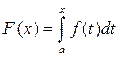обладает свойствами:

1) непрерывна на [ a; b ];

2) имеет производную F' (x) в каждой точке x Î [ a; b ], удовлетворяющую равенству .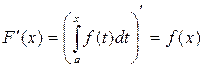

Доказательство: Вычислим приращение функции F (x), причем D x возьмем таким, чтобы точка x + D x Î [ a; b ].

Тогда

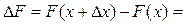
Применим к полученному интегралу теорему о среднем значении определенного интеграла. То есть на [ x; x + Dx ] существует такое число c, в котором выполняется равенство:

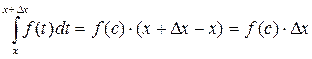
Значит, D F = f (c)× Dx, где c Î [ x; x + Dx ].

Если Dx ® 0, то c ® x (так как x < c < x+Dx).

Поэтому, в силу непрерывности f (x), получим f (c) ® f (x) при Dx ®0.

Таким образом, DF ®0 при Dx ®0, что доказывает непрерывность F (x).

Кроме того, вычисляя предел отношения DF к Dx при Dx ® 0, получим:

То есть существует конечный предел отношения DF к Dx при Dx ®0. Что означает существование производной F' (x) = f (x).

Из этой теоремы следует, что функция 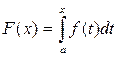является первообразной для функции f (x).