Пример 3. Интегрирование по частям в определенном интеграле

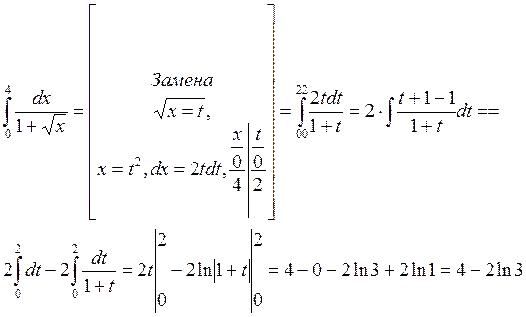
Ответ: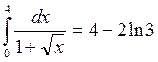

Пример 4.

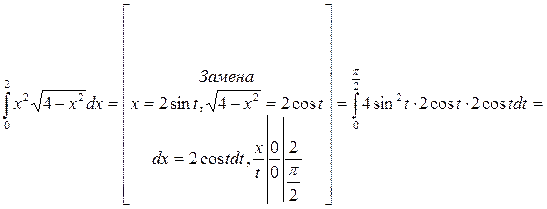
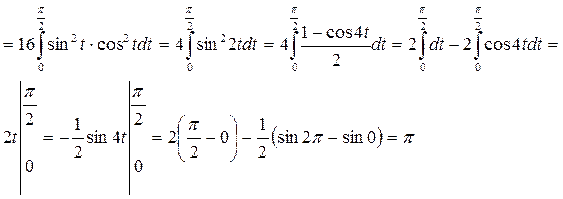
Ответ: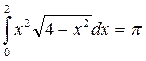

Интегрирование по частям в определенном интеграле

Теорема 6. Пусть функции u (x) и V (x) имеют непрерывные производные на [ a; b ]. Тогда справедливо равенство:

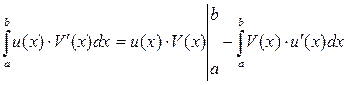
Доказательство.

Так как (u (x)× V (x))' = u (x) V' (x) + u' (x)× V (x) для любого x Î [ a; b ], то функция u (x)× V (x) является одной из первообразных функции

u (x) V' (x) + u' (x) V (x).

Поэтому по формуле Ньютона-Лейбница:

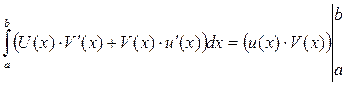
Пользуясь свойством определенного интеграла можно это равенство записать в виде:

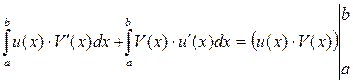
Отсюда следует:

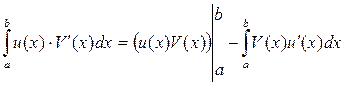
Эту формулу удобно записать в виде:

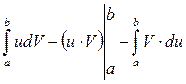
Пример 5.

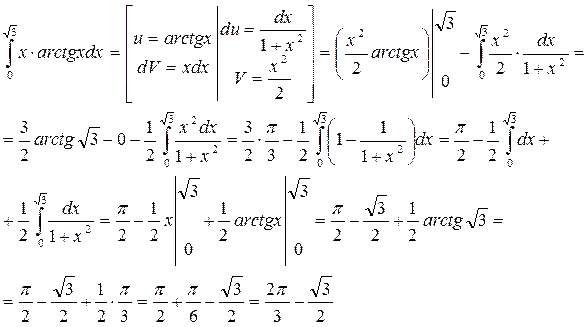
Ответ:

Пример 6.

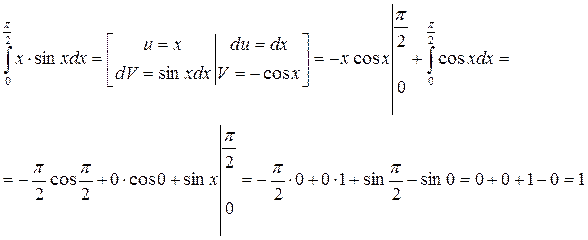
Ответ: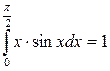

ГЛАВА 6. ГЕОМЕТРИЧЕСКИЙ смысл определенного интеграла. Нахождение площадей фигур, и параметров, необходимых для анализа данных (средних значений, длин кривых и т.п.).

(слайды 15-21 в презентации)