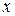Несобственные интегралы

· Интегралы с бесконечными пределами интегрирования называются несобственными интегралами.

Несобственным интегралом с бесконечным пределом интегрирования (интегралом 1-го рода) называется предел интеграла 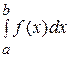при :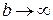

.

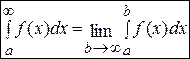Если этот предел существует и конечен, то несобственный интеграл называется сходящимся, а если предел не существует или равен 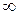, то расходящимся.

Пусть - первообразная функция для 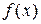на промежутке 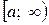. Тогда можно применить формулу Ньютона-Лейбница:

.

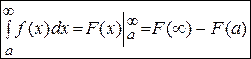Пример. .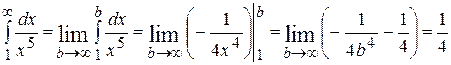

Данный интеграл является сходящимся.

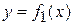
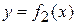
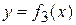
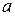
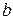
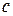
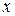
Если фигура 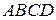не является криволинейной трапецией, то представляют ее как сумму криволинейных трапеций: .

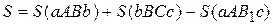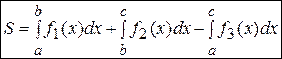
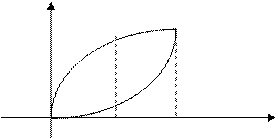
Пример. Вычислить площадь фигуры, ограниченной графиками функций , , , .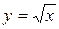

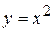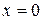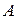
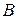
½ 1