
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сызықтық регрессия
|
|
Регрессия функциясының, яғ ни 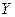 - тің
- тің 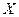 - ке (немесе
- ке (немесе 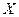 - тің
- тің 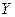 - ке) тә уелділігінің моделінің тү рін таң дап алғ аннан кейін, мә селен,
- ке) тә уелділігінің моделінің тү рін таң дап алғ аннан кейін, мә селен, 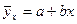 сызық тық моделін, моделдің коэффициенттерінің нақ ты мә ндерін анық тау қ ажет.
сызық тық моделін, моделдің коэффициенттерінің нақ ты мә ндерін анық тау қ ажет.
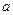 жә не
жә не 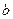 ә ртү рлі мә ндері бойынша
ә ртү рлі мә ндері бойынша 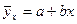 тү ріндегі шексіз кө п тә уелділікті алуғ а болады, яғ ни координата жазық тығ ындағ ы шексіз кө п тү зулер тұ рғ ызуғ а болады, ал бізге бақ ылап отырғ ан мә ндерге ө те жақ ын, ең тиімді тү рде сә йкес келетін тә уелділік қ ажет. Яғ ни, ең жақ сы коэффициенттерді таң дау керек.
тү ріндегі шексіз кө п тә уелділікті алуғ а болады, яғ ни координата жазық тығ ындағ ы шексіз кө п тү зулер тұ рғ ызуғ а болады, ал бізге бақ ылап отырғ ан мә ндерге ө те жақ ын, ең тиімді тү рде сә йкес келетін тә уелділік қ ажет. Яғ ни, ең жақ сы коэффициенттерді таң дау керек.
Ең кіші квадраттар ә дісі (ЕКӘ)
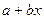 сызық тық функциясын бақ ылау нә тижесінде алынғ ан мә ндерге қ атысты іздейміз. Бақ ылау мә ндеріне ө те жақ ын сә йкес келетін функцияны табу ү шін ең кіші квадраттар ә дісін қ олданамыз.
сызық тық функциясын бақ ылау нә тижесінде алынғ ан мә ндерге қ атысты іздейміз. Бақ ылау мә ндеріне ө те жақ ын сә йкес келетін функцияны табу ү шін ең кіші квадраттар ә дісін қ олданамыз.
Мынадай белгілеулер енгіземіз: 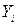 -
- 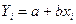 тең деуі бойынша есептелінген мә ндер,
тең деуі бойынша есептелінген мә ндер,
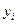 - бақ ылау нә тижесінде ө лшелініп алынғ ан мә ндер,
- бақ ылау нә тижесінде ө лшелініп алынғ ан мә ндер,
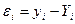 - ө лшелініп алынғ ан мә ндер мен тең деу бойынша есептелінген мә ндердің айырмасы,
- ө лшелініп алынғ ан мә ндер мен тең деу бойынша есептелінген мә ндердің айырмасы, 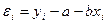 .
.
Ең кіші квадраттар ә дісінде ө лшелініп алынғ ан 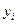 мә ндері мен тең деу бойынша есептелінген
мә ндері мен тең деу бойынша есептелінген 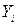 мә ндерінің айырмасы ең аз (минимальды) болуы талап етіледі. Яғ ни, а жә не
мә ндерінің айырмасы ең аз (минимальды) болуы талап етіледі. Яғ ни, а жә не 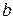 коэффициенттерін бақ ылап отырғ ан мә ндердің тү зу сызық ты регрессияның мә ндерінен ауытқ уының квадраттарының қ осындысы ө те аз болатындай етіп іздейміз:
коэффициенттерін бақ ылап отырғ ан мә ндердің тү зу сызық ты регрессияның мә ндерінен ауытқ уының квадраттарының қ осындысы ө те аз болатындай етіп іздейміз:
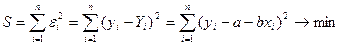 .
.
Бұ л 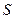 - фукнкциясы а жә не
- фукнкциясы а жә не 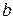 аргументтеріне тә уелді екі айнымалының функциясы болып табылады.
аргументтеріне тә уелді екі айнымалының функциясы болып табылады. 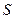 - функциясын туындының кө мегі арқ ылы экстремумғ а зерттей отырып, бұ л функция минимальды мә нді, егер а жә не
- функциясын туындының кө мегі арқ ылы экстремумғ а зерттей отырып, бұ л функция минимальды мә нді, егер а жә не 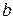 коэффициенттері мынадай жү йенің шешімі болғ ан жағ дайда қ абылдайтынын дә лелдеуге болады.
коэффициенттері мынадай жү йенің шешімі болғ ан жағ дайда қ абылдайтынын дә лелдеуге болады.
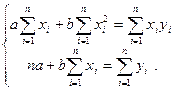 (*)
(*)
Бұ л жү йе ең кіші квадраттар ә дісінің қ алыпты тең деулер жү йесі деп аталады.
Егер қ алыпты тең деулердің екі жағ ын да n – ге бө лсек, онда
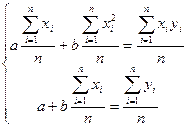
аламыз.
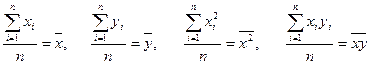 , (**)
, (**)
екенін ескерсек,
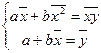
аламыз. Бұ дан 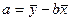 , а- ның мә нін бірінші тең деуге қ ою арқ ылы
, а- ның мә нін бірінші тең деуге қ ою арқ ылы
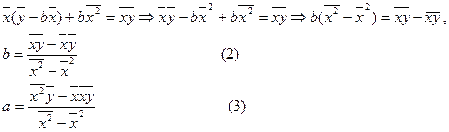
аламыз. 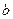 - регрессия коэффициенті, а- регрессия тең деуінің бос мү шесі.
- регрессия коэффициенті, а- регрессия тең деуінің бос мү шесі.
Алынғ ан тү зу теориялық регрессия сызығ ының бағ асы болып табылады.
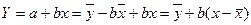 .
.
Сонымен, 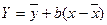 сызық тық регрессияның тең деуі.
сызық тық регрессияның тең деуі.
Регрессия тура 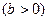 жә не кері
жә не кері 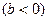 болуы мү мкін.
болуы мү мкін.
Егер бірінші параметрдің мә ндері ө скенде, екінші параметрдің мә ндері ө сетін болса, онда ол тура регрессия, ал бір параметрдің мә ндері ө скенде, екінші параметрдің мә ндері кемитін болса, онда ол – кері регрессияны білдіреді.
1-мысал. n елді мекендерінде тә улігіне тұ щы суды санитарлы-тұ рмыстық мұ қ таждық қ а пайдаланудың Х (л/адам) берілген дең гейіне жалпы ауру-сырқ аулық тың 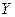 (%) дең гейінің кө птеген мә ні сә йкес келеді. (% - ке шақ қ анда). Бұ л жағ дайда Х-тің ө суіне
(%) дең гейінің кө птеген мә ні сә йкес келеді. (% - ке шақ қ анда). Бұ л жағ дайда Х-тің ө суіне 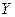 - ң кемуісә йкес келетіні байқ алады. Бұ л – кері, теріс корреляциялық байланыс. (1 сурет).
- ң кемуісә йкес келетіні байқ алады. Бұ л – кері, теріс корреляциялық байланыс. (1 сурет).
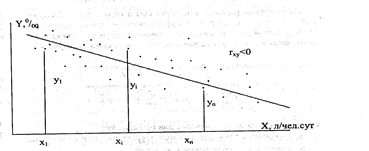 |
1-сурет. Х факторы мен 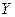 параметрінің арасындағ ы кері корреляциялық байланысты бақ ылау ө рісі.
параметрінің арасындағ ы кері корреляциялық байланысты бақ ылау ө рісі.
 |
2-мысал. Ө ндіріс аймағ ындағ ы жұ мыс орнының тығ ыздығ ы Х (адам) ө скен сайын жұ қ палы ауру дең гейінің
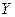 (% пен) ө суі – тура, оң корреляциялық байланыстың мысалы болып табылады (2 сурет).
(% пен) ө суі – тура, оң корреляциялық байланыстың мысалы болып табылады (2 сурет).
2-сурет.Х факторы мен 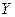 параметрінің арасындағ ы тура корреляциялық байланысты бақ ылау ө рісі.
параметрінің арасындағ ы тура корреляциялық байланысты бақ ылау ө рісі.