
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнения Бернулли для невязкой жидкости
|
|
Геометрическое и энергетическое истолкование
уравнения Бернулли для невязкой жидкости
Проясним геометрический смысл уравнения Бернулли (4.27) для элементарной струйки идеальной жидкости:
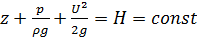 .
.
Все слагаемые уравнения имеют размерность длины.
Член уравнения z определяет высоту центра тяжести рассматриваемого сечения над горизонтальной плоскостью сравнения. Его называют геометрической высотой или геометрическим напором.
Член уравнения p/ρ g называют пьезометрической высотой или пьезометрическим напором.
Член уравнения U 2/2 g называют скоростной высотой или скоростным напором.
Трёхчленная сумма H - полный (гидродинамический) напор в данном сечении струйки.
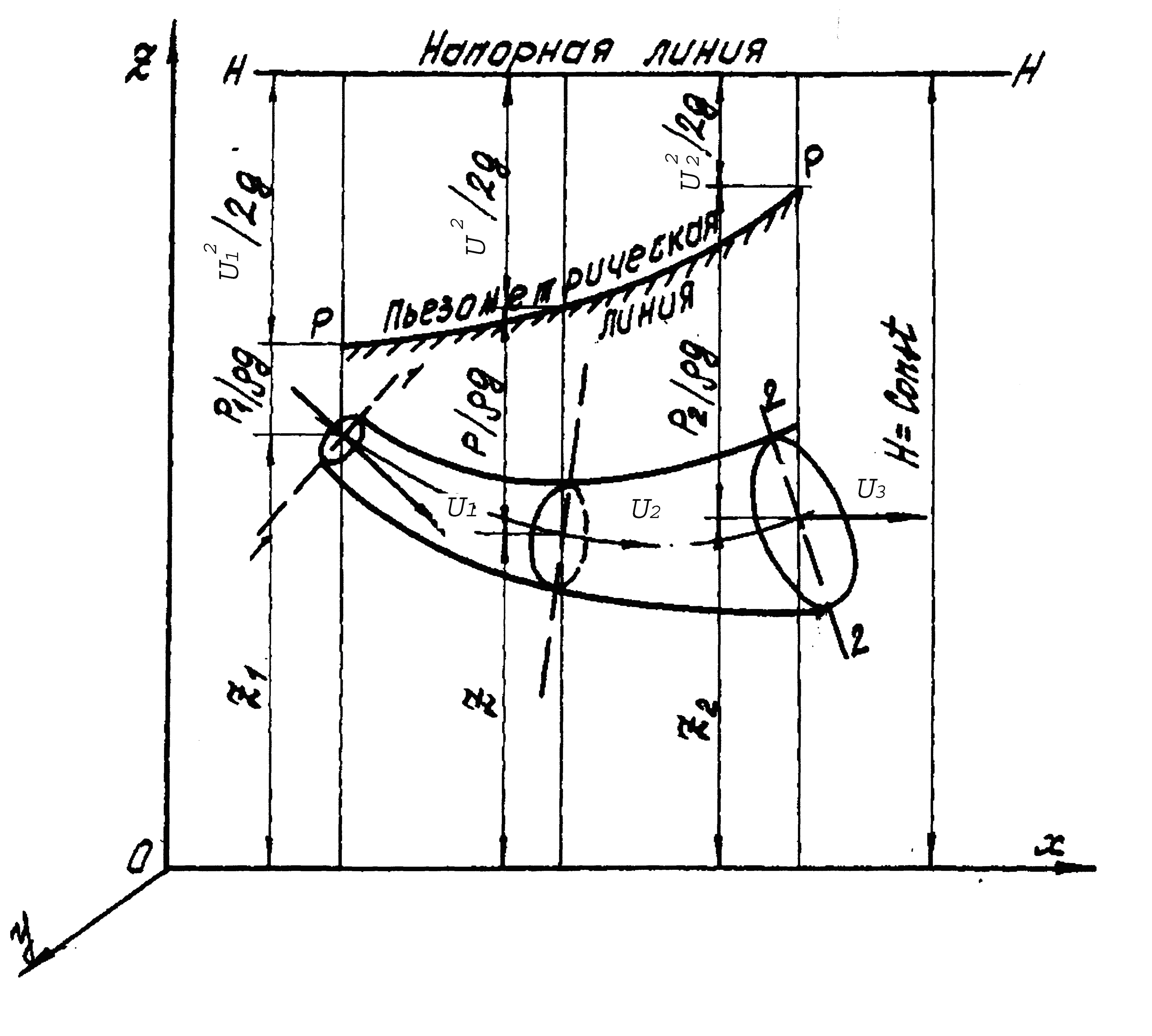 Рис. 4.3
Рис. 4.3
|
Соединив концы отрезков, выражающих скоростные напоры U 2/2 g, получим линию H-H, называемую напорной или линией полного напора.
Соединив концы отрезков, выражающих пьезометрические высоты p/ρ g, получим пьезометрическую линию Р-Р. Эта линия изображает изменение суммы геометрической и пьезометрической высот вдоль струйки.
Рассмотрим механический смысл уравнения Бернулли для элементарной струйки идеальной жидкости. Напишем уравнение для двух произвольных сечений 1-1 и 2-2:
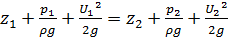 . (4.27)
. (4.27)
Перегруппировав члены уравнения, придадим ему вид:
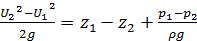 . (4.28)
. (4.28)
Получили уравнение кинетической энергии для единицы веса жидкости. Слагаемые в правой части (4.28) выражают работы удельных сил тяжести и давления. Левая часть уравнения представляет приращение кинетической энергии жидкости единичного веса.
Таким образом, слагаемые уравнения Бернулли выражают работу единицы веса жидкости, так как удельные работы эквивалентны удельным энергиям. Следовательно:
z - удельная (потенциальная) энергия положения,
p/ρ g - удельная (потенциальная) энергия давления,
z + p/ρ g - удельная потенциальная энергия,
U 2/2 g - удельная кинетическая энергия.
Из (4.27) следует, что полная удельная энергия H постоянна вдоль струйки идеальной жидкости.