Уравнение Бернулли для струйки реальной жидкости

Напишем уравнения Навье-Стокса для струйки при установившемся движении (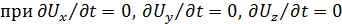, то есть при отсутствии локальных ускорений):

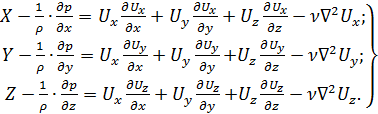(4.29)

Для всех точек на оси струйки согласно уравнениям линии тока

; .

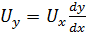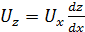Используя эти выражения, преобразуем первое уравнение системы (4.29)

,

а затем умножим его на dx.

Тогда, после сокращений, вынесения 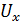за скобки и преобразований:

.

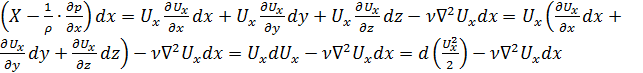Аналогично преобразуем второе и третье уравнения системы (4.29):

;

.

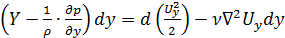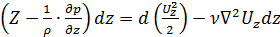Пусть объемные силы, действующие на жидкость, имеют потенциал Π:

; ; .

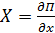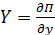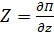Тогда, сложив и преобразовав эти уравнения, получим

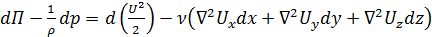. (4.30)

Второе слагаемое в правой части уравнения (4.30) выражает работу dA, затраченную на преодоление сил вязкости при перемещении единицы массы жидкости на расстояние dS, то есть

.

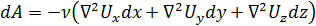Используя введённое обозначение, перепишем уравнение (4.30) в виде

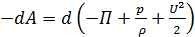. (4.31)

Проинтегрировав (4.31) на участке между сечениями 1-1 и 2-2 (рис. 4.4), получим уравнение Д. Бернулли для струйки реальной жидкости:

,

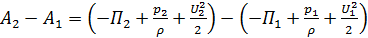или

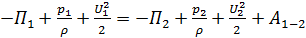. (4.32)

Величина A _1-2 = A ₁ -A ₂ - это энергия, потерянная единицей массы жидкости на участке между сечениями 1-1 и 2-2. Определить величину A _1-2 в общем случае трудно из-за сложности интегрирования уравнения Навье-Стокса.

Рассмотрим важный частный случай, когда жидкость движется в поле силы тяжести, и другие массовые силы на неё не действуют. Тогда П= -gz.

Потерянная работа, совершаемая единицей веса жидкости против сил сопротивления при перемещении её из сечения 1-1 в сечение 2–2 (рис. 4.4):

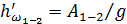. (4.33)

Поэтому, разделив уравнение (4.32) на g, получим в окончательном виде уравнение Бернулли для струйки реальной жидкости:

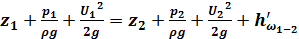. (4.34)

Как видим, в случае реальной жидкости полный напор вдоль струйки не остаётся постоянным, а убывает в направлении движения. Поэтому график уравнения Бернулли для струйки реальной жидкости (рис. 4.4) отличается от аналогичного графика для идеальной жидкости (рис. 4.3).