Уравнение Бернулли для потока реальной жидкости

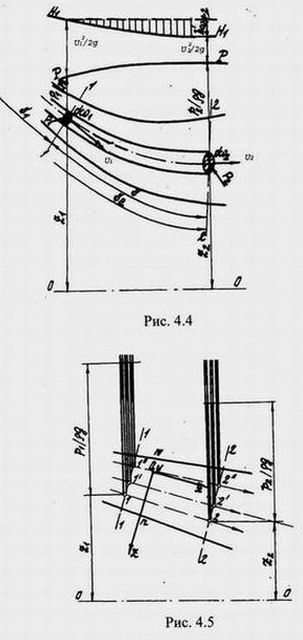
Углы между линиями тока малы, и поперечные компоненты скорости малы, поэтому можно принять 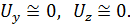Из уравнения неразрывности (3.17) следует, что . Пренебрегая в уравнениях Навье-Стокса (4.29) членами, зависящими от U_y и U_z, получим:

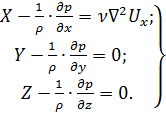(4.35)

Так как последние два уравнения системы (4.35) не отличаются от уравнений равновесия жидкости (2.7), можно заключить, что при плавно изменяющемся движении в пределах живого сечения потока давление распределяется по гидростатичес-кому закону. Это означает, что при плавно изменяющемся движении в разных точках живого сечения величины z и p/ρ g имеют разные значения, однако их сумма (пьезометрический напор) постоянна:

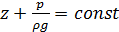. (4.36)

В другом живом сечении сумма z+p/ρ g будет иная, но постоянная для всех точек сечения. Этот результат позволяет распространить уравнение Бернулли на поток конечных размеров.

Соблюдая условие плавной изменяемости при переходе к потоку жидкости, будем исходить из (4.34). Умножив (4.34) на весовой расход струйки ρ gdQ, получим уравнение, выражающее энергию элементарной струйки:

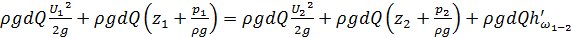. (4.37)

Суммируя энергии струек по живому сечению потока, получим энергию всего потока:

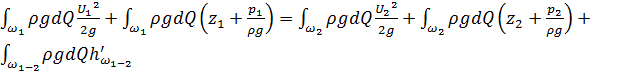. (4.38)

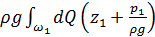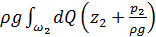В (4.38) члены и выражают потенциальную энергию потока (в сечениях 1-1 и 2-2), которой обладает масса жидкости, проходящая через живое сечение в единицу времени.

Потенциальная энергия для произвольного сечения

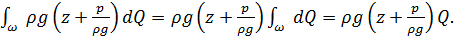
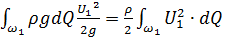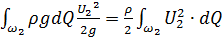Члены (4.38) и выражают кинетическую энергию массы жидкости, протекающей через живые сечения 1–1 и 2–2 потока в единицу времени. Рассмотрим эти слагаемые более подробно. Так как для произвольного сечения струйки

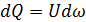, то .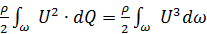

Скорость в отдельной (любой) струйке можно представить в виде суммы средней скорости 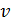в живом сечении потокаи её отклонения ε от средней: 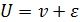. Сделав подстановку, получим для кинетической энергии потока:

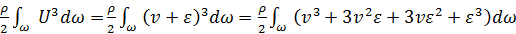или

.

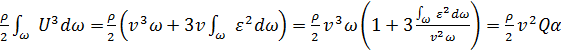Здесь учтено, что 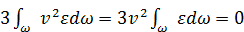, так как 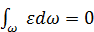, а 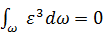, так как ε мало и для разных точек сечения имеет разные знаки. Кроме того, произведена замена и обозначено 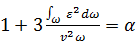. Отсюда

.

Величина α - коэффициент Кориолиса (корректив кинетической энергии) - отношение действительной кинетической энергии потока к кинетической энергии, которой обладал бы поток при том же расходе, если бы все частицы жидкости двигались с одной и той же (средней) скоростью. Коэффициент α зависит от степени неравномерности распределения скоростей по сечению. Для ламинарного течения в круглой цилиндрической трубе α =2, для турбулентного течения α ≈ 1.05÷ 1.1.

Однако при существенной неравномерности эпюры скоростей коэффициент α может оказаться и более значительным.

Последнее в (4.38) слагаемое 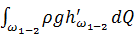, выражающее потерю энергии потоком за единицу времени при перемещении его из сечения 1–1 в сечение 2–2, можно (усреднив потери в струйках по сечению потока) представить в виде

.

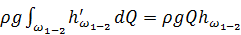Подставляя полученные выражения в уравнение (4.38), получим:

.

После сокращения на ρ gQ

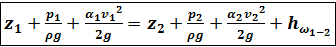. (4.39)

Выражение (4.39) - уравнение Бернулли для потока однородной вязкой несжимаемой капельной жидкости при установившемся плавно изменяющемся движении.

Уравнение (4.39) выражает закон изменения кинетической энергии применительно к одномерным задачам гидромеханики.

Уравнение (4.39) выведено при условии плавной изменяемости потока в выбранных расчетных сечениях. На участке потока между сечениями это условие может нарушаться.

Последний член правой части уравнения (4.39) выражает усредненную потерю удельной механической энергии (потерю напора) между сечениями 1–1 и 2–2.

Уравнению (4.39) можно дать геометрическую трактовку, построив график (диаграмму) уравнения Бернулли для потока вязкой жидкости (рис. 4.6).