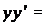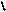Айнымалылары ажыратылатын жəне ажыратылған бірінші ретті дифференциалдық теңдеулер
Дифференциалдық тең деулердің дұ рыс шешімдерін табу ү шін интеграл мен туынды тарауларына қ айталап шолу жасауды қ ажет етеді.
2.1.1 Анық тама:
P(x, y)dx+Q(x, y)dy=0 (5)
бірінші ретті тең деу айнымалылары ажыратылатын дифференциалдық тең деу деп аталады.
Егер P и Q функциялары тек бір ғ ана айнымалылардан тə уелді кө пмү шеліктерге жіктелінсе жə не
f1(x)· f2(y)dx+φ 1(y) ·φ 2(y)dy=0 (6)
тең деу мү шелерін f2(y)·φ 1(х)-ке бө лсек айнымалылары ажыратылады.
f 1(x) ϕ 2(y) 
ϕ 1(x) f 2(y)
Тең деу мү шелерін интегралдай отырып ізделінді жалпы интегралды табамыз:
f 1(x) ϕ 2 (y) 
ϕ 1(x) f 2 (y)
(xy2+x)dx+(y-x2y)dy=0 дифференциалдық тең деуінің  жалпы шешімін табың ыз.
Шешімі: берілгені 1-ші ретті айнымалылары ажыратылатын тең деу. Кө пмү шеге жеткізсек тең деу
x (y + 1) dx + y (1 - x) dy = 0
тү ріне келеді. Мү шелеп (1-х2) (у2+1)-ге бө лсек
тең деу (7) тү ріне келеді. Енді мү шелеп 
интегралдаймыз
x 
1- x 2
1 d (1- x 2 ) 1 
2 1- x 2 2
-ln 1- x 2 + ln 1+ y 2 
= ln C ⇒ 1+ y 2 = C (1- x 2)
демек-жалпы шешімі.
дифференциалдық тең деуінің жалпы 
y = ± C (1 - x) - 1  
интегралын анық тайық.
Шешімі:
екенін біле отырып 
dy 1- 2 x 
dx y
Тең деудің екі бө лігін де
dy 1- 2 x 
dx y
y 2 dу = (1- 2 x) dx
Мү шелеп интегралдайық:
y dу = (1- 2 x) dx
3
= x - x + C 
-жалпы интегралы.
+ x - x
Мысалы 3: у ′ Sinx=ylny, 
анық таң ыз.
Шешімі:
а) жалпы шешімін ізделік:
Sinx = y ln y 
Sinxdy = y ln ydx
Тең деудің екі бө лігін де бө лелік: | Sinx ⋅ y ln y ≠ 0
dx
Sinx
| |
dy 
y ln y
Мү шелеп интегралдайық
d (ln y) | lnln y = ln tg
ln y = tg ⋅ C
| | 
ln y
+ln C
- жалпы шешімі.
анық тайық. Ол ү шін берілген бастапқ ы 
шартын қ олданамыз. Шарттың берілгендерін 
табылғ ан жалпы шешімге қ оямыз. Сонда
c ⋅ tg 
-тұ рақ тының мə ні.
c = 1
б) ізделінді c=1 тұ рақ тысын жалпы шешімдегі орнына енгізе отырып
-дербес шешімге ие боламыз.
|
