Уравнение (3), не содержащее реакции оси рычага, выражает условие, которому удовлетворяют задаваемые силы, приложенные к рычагу, если он находится в покое.

Это условие формулируется так: если рычаг находится в покое, то алгебраическая сумма моментов всех задаваемых сил, приложенных к рычагу, относительно опорной точки равна нулю:

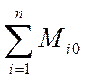=0

Из уравнений (1) и (2) равновесия определяются модуль и направле­ние реакции оси рычага. Из условия, которое выполняется, если рычаг находится в покое, получим условие устойчивости тел при опро­кидывании.

Положим, что к прямоугольному параллелепипеду (рисунок) весом 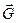на высоте d приложена горизонтальная сила 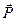, которая может не только сдвинуть тело, но и опрокинуть его при вращении вокруг ребра А. Считая, что сила 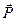недостаточно велика, чтобы сдвинуть тело, рассмотрим ее опрокидывающее действие. Обозначим а расстояние от точки А, изображающей на чертеже ось вращения рычага, до линии действия силы 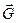, которая препятствует опрокидыванию.

Составим сумму моментов задаваемых сил 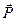и 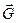относительно опорной точки А:

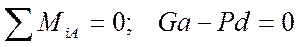, откуда .

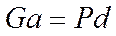Назовем абсолютные значения моментов сил 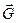и 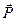относительно точки А удерживающим и опрокидывающим моментами:

.
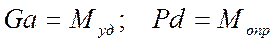