Метод Эйлера

Для получения приближенного решения системы дифференциальных уравнений заменим производную простейшей конечно-разностной формулой:

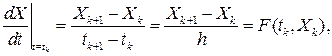
где h – шаг интегрирования.

Тогда

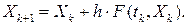
Известно, что метод Эйлера является ограниченно устойчивым, то есть существует критический шаг интегрирования 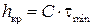, где 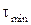– минимальная постоянная времени динамической системы, описываемой исследуемыми дифференциальными уравнениями, а С =2.

В качестве примера будем рассматривать двигатель типа 2ПБ200LУХЛ4.

– номинальная мощность: Р _Н=15 кВт;

– номинальное напряжение: U _Н=220 В;

– номинальное значение скорости вращения двигателя:

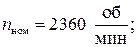
– КПД: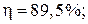

– сопротивление обмотки якоря при температуре 15⁰С:

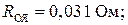
– сопротивление обмотки дополнительных полюсов при температуре 15⁰С: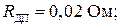

– индуктивность двигателя: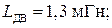

– момент инерции двигателя: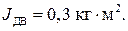

Задаем параметры двигателя в MathCAD:

Номинальный ток:

Номинальная угловая частота вращения:

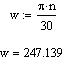
Активное сопротивление обмотки якоря в «горячем» состоянии:

Коэффициент связи двигателя:

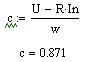
Скорость идеального холостого хода:

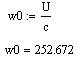
Номинальный электромагнитный момент:

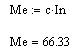
Номинальный момент:

Момент трения на валу двигателя:

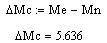
Число точек расчета:

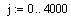
Шаг расчета:

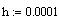
Нулевые начальные условия:

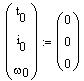
Алгоритм метода Эйлера:

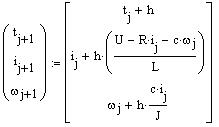
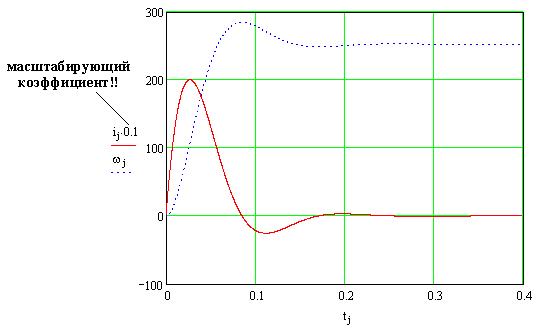
Рис.4. Переходные процессы в ДПТ НВ при решении СДУ методом Эйлера