Систем дифференциальных уравнений. Предположим, что ЭМС описывается неоднородной СДУ в нормальной форме Коши:

Предположим, что ЭМС описывается неоднородной СДУ в нормальной форме Коши:

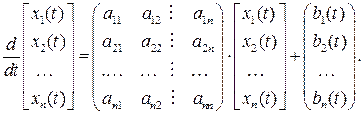
с ненулевыми начальными условиями

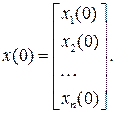
Применим к СДУ прямое преобразование Лапласа. Учитывая теорему дифференцирования оригинала

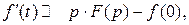
получим следующую СЛАУ:

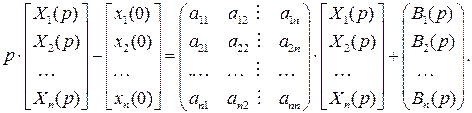
Перенесем слагаемые с неизвестными в левую часть СЛАУ, а свободные члены в правую:

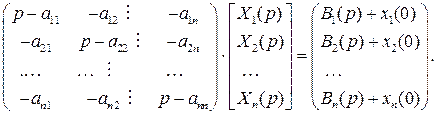
При нулевых начальных условиях данная СЛАУ выглядела бы следующим образом:

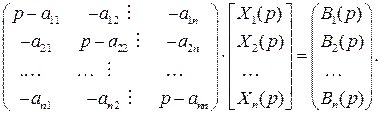
Преобразование Лапласа позволяет учесть начальные условия на самом первом этапе решения СДУ, при этом полученная СЛАУ ненамного отличается от той же СЛАУ при нулевых начальных условиях. В этом заключается одно из существенных преимуществ операторного метода решения СДУ перед классическим, в котором для учета начальных условий и нахождения постоянных интегрирования составлялась и решалась отдельная СЛАУ.

СДУ для ДПТ НВ в матричном виде:

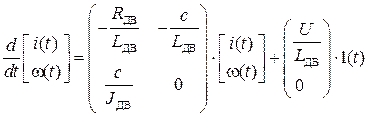
Применяя к этой СДУ прямое преобразование Лапласа с нулевыми начальными условиями, получаем СЛАУ следующего вида:

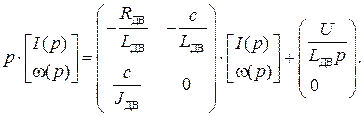
Перенесем слагаемые с неизвестными в левую часть СЛАУ:

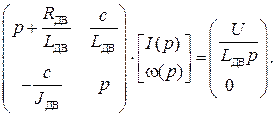
В программной среде MathCAD:

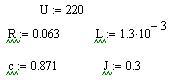
Операторные матрицы:

Решение операторной системы уравнений методом обратной матрицы:

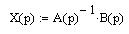
Применяя обратное преобразование Лапласа, получаем временные зависимости тока якоря и скорости вращения вала двигателя.

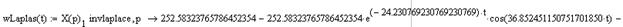
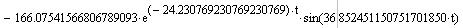
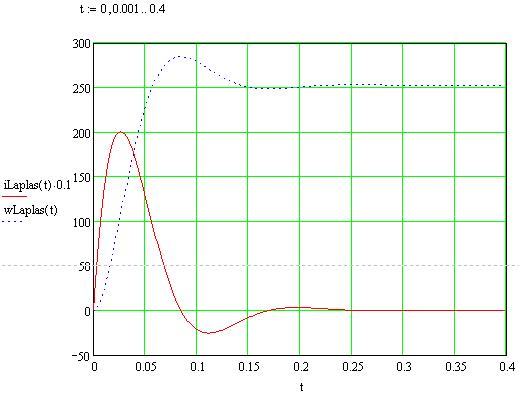
Рис.6. Переходные процессы в ДПТ НВ при решении СДУ операторным методом