Систем дифференциальных уравнений

Пусть ЭМС описывается некоторой неоднородной СДУ, и в зависимости от режима работы ЭМС заданы начальные условия 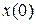для переменных состояния 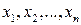. Тогда для этой СДУ решение задачи Коши классическим способом может быть найдено по следующему алгоритму:

1. Выписать однородную систему, соответствующую заданной неоднородной, и найти ее общее решение .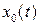

2. Найти частное решение 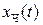неоднородной системы.

3. Записать общее решение в виде суммы: .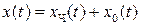

4. Найти частное решение неоднородной СДУ, удовлетворяю­щее заданным начальным условиям .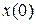

Другими словами четвертый этап состоит в нахождении постоянных интегрирования. Несмотря на то, что в классическом курсе математики постоянные интегрирования обозначают через букву C, будем обозначать постоянные интегрирования буквой N для того, чтобы не перепутать их с ёмкостью конденсатора или коэффициентом связи двигателя постоянного тока.

Пункт 1. При решении однородных СДУ наиболее удобным является метод сведения решения системы к задаче отыскания собственных значений и собственных векторов матрицы коэффициентов СДУ. Его алгоритм следующий:

1. Записать матрицу A коэффициентов перед неизвестными СДУ.

2. Найти собственные значения и собственные вектора матрицы A. При этом число полученных линейно независимых собственных векторов матрицы A должно равняться порядку СДУ. В противном случае система должна решаться другим методом (например, метод исключения неизвестных или метод неопределенных коэффициентов).

3. Выписать все компоненты решения СДУ в зависимости от типа корней.

Алгоритм нахождения собственных значений и собственных векторов матрицы A:

1. Записать уравнение , где E – единичная матрица:

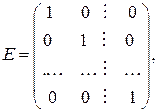
λ – собственные значения матрицы A, и решить его. Данное уравнение называется характеристическим.

2. Для каждого полученного собственного значения 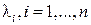, составить систему линейных алгебраических уравнений (СЛАУ):

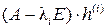
или

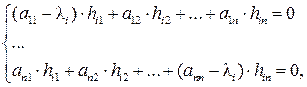
где – собственный вектор, соответствующий собственному значению .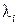

3. Решить систему для каждого значения 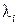, то есть найти собственный вектор 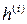, соответствующий каждому собственному значению.