Правило 2. Корни характеристического уравнения комплексные, различные

Если среди корней характеристического уравнения есть комплексный корень 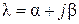, а значит, и сопряженный ему корень 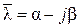(по свойству алгебраических уравнений с действительными коэффициентами), то компонента общего решения системы, соответствующая этой паре 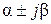корней, записывается в виде

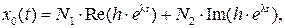
где 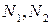– произвольные постоянные.

СДУ, описывающая ДПТ НВ, в матричном виде:

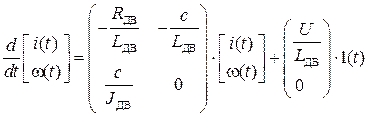
Зададим параметры ДПТ в MathCAD:

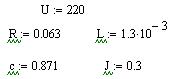
Матрицы параметров и единичная матрица:

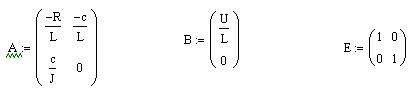
Корни характеристического уравнения:

Корни комплексно сопряженные, значит достаточно определить собственный вектор только для одного из них. Найдем собственный вектор матрицы A для значения 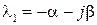из системы уравнений :

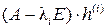Примем для удобства 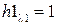и найдем 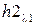из второго уравнения получившейся системы, являющегося наиболее простым:

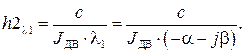
В MathCAD:

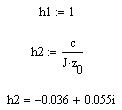
Общее решение однородной СДУ:

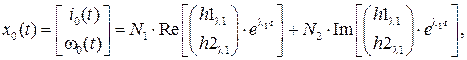
где 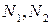– постоянные интегрирования.

Пункт 2. Частное решение неоднородной СДУ физически представляет собой статический режим работы ЭМС, то есть состояние при 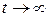. Исходя из этого, частное решение неоднородной СДУ, можно получить при подстановке в СДУ значения 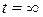. Как известно, при этом производные обращаются в ноль, и СДУ превращается в систему алгебраических уравнений (СЛАУ), которую можно решить одним из методов линейной алгебры.

Найдем частное решение неоднородной СДУ при :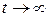

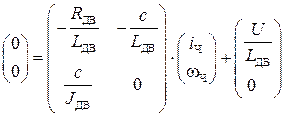
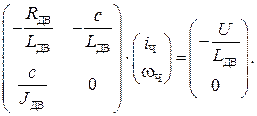
Решим полученную СЛАУ в MathCAD методом обратной матрицы:

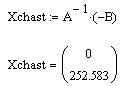
Полученное частное решение является физически адекватным, так как при пуске вхолостую ток двигателя устанавливается на нулевом значении, а двигатель разгоняется до скорости идеального холостого хода.

Пункты 3 и 4. Для нахождения частного решения неоднородной СДУ, удовлетворяющего заданным начальным условиям 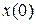, необходимо записать общее решение в виде суммы 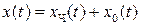, а затем подставить в него значения 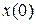. В результате этой подстановки получится СЛАУ, в которой неизвестными будут выступать постоянные интегрирования 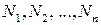. Полученную СЛАУ можно решить любым известным методом линейной алгебры.

Общее решение СДУ:

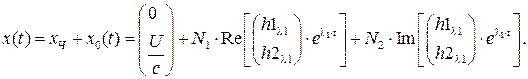
Найдем постоянные интегрирования при нулевых начальных условиях: .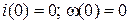

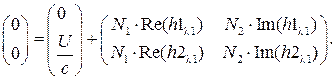
Решение СЛАУ в MathCAD методом обратной матрицы:

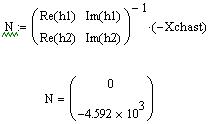
Отметим, что при работе ДПТ НВ на холостом ходу первая постоянная интегрирования равна нулю.

Запишем получившиеся зависимости тока и скорости от времени.

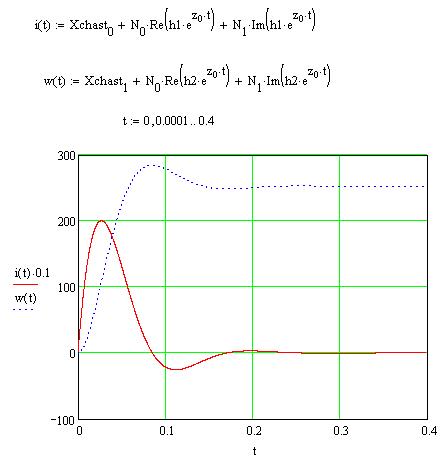
Рис.5. Переходные процессы в ДПТ НВ при решении СДУ классическим методом