Визначення параметрів рівняння регресії. Регресійний аналіз

Параметри рівняння регресії 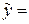f(x) зазвичай знаходяться за методом найменших квадратів, який забезпечує такий вибір їх числових значень, щоб сума квадратів відхилень емпіричних значень у_і ознаки Y від відповідних теоретичних (або вирівняних) значень 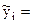f(x_і) була найменшою:

.

Зокрема, для лінійного 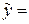а+bх та квадратичного 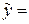р+qx+rx ² рівнянь регресії параметри знаходяться із систем лінійних алгебраїчних рівнянь відповідно

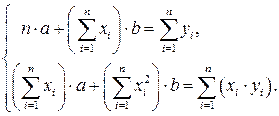(3.9)

та

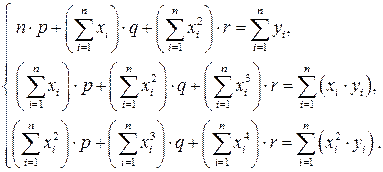(3.10)

Величина

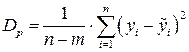, (3.11)

де п – число пар (х_і; у_і), m – число параметрів рівняння регресії, які знаходяться за даними вибірки, називається регресійною дисперсією і може слугувати критерієм вибору виду рівняння регресії.

При цьому необхідно враховувати таке. Якщо значення варіант х_і та у_і є достатньо великими числами, то деякі коефіцієнти при невідомих (наприклад, 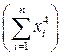у системі (3.10)) можуть мати число значущих цифр, яке перевищує число робочих розрядів у процесорах технічних засобів обчислень, що унеможливлює проведення обчислень. У таких ситуаціях необхідно перейти до умовних варіант 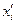та 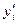за формулами

, ,

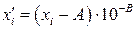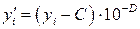де число А обирається дослідником довільно, але бажано якомога ближче до середини інтервалу (х_тіп; х_тах) з урахуванням зручності подальших обчислень (наприклад, обираючи А кратним 10); В – довільне ціле невід’ємне число, яке визначає порядок величин 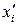. Аналогічно вибираються значення чисел С та D. Якщо при цьому виникла необхідність вибирати значення В або D більшими від нуля, то числа 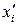або 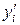можна (але не бажано) округлювати, зменшуючи тим самим їх число значущих цифр.

Після переходу до умовних варіант 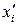та 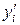із систем виду (3.9) та (3.10) можна знайти умовні параметри 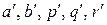, в результаті чого одержимо умовні рівняння регресії

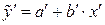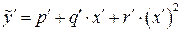, . (3.12)

Для переходу до фактичних варіант і параметрів та одержання фактичних рівнянь регресії необхідно в умовні рівняння регресії (3.12) замість змінних 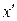та 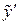підставити їх вирази через відповідно х та :

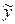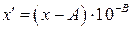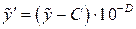, . (3.13)

В результаті одержимо шукані рівняння регресії

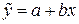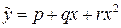, . (3.14)

Для хоча б часткової перевірки останніх необхідно побудувати їх графіки на кореляційному полі (рис. 3.6) і візуально переконатись у тому, що точки (х_і; у_і) кореляційного поля розташовані хоча б приблизно порівну і рівномірно по обидва боки графіка. У противному разі є підстави сумніватись щодо правильності обчислення параметрів (або побудови графіка).