Метод Ньютона решения нелинейного уравнения. Геометрический смысл метода Ньютона

Лекция 20. Нелинейные уравнения и методы их решения (продолжение)

План

Метод Ньютона решения нелинейного уравнения. Геометрический смысл метода Ньютона

Скорость сходимости метода Ньютона, преимущества и недостатки

Метод хорд решения нелинейного уравнения. Геометрический смысл

Скорость сходимости метода хорд. Преимущества и недостатки

Метод простой итерации решения нелинейного уравнения. Скорость сходимости

Метод Ньютона решения нелинейного уравнения. Геометрический смысл метода Ньютона

Пусть решается нелинейное уравнение

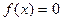. (1)

Предположим, что 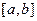содержит единственный корень уравнения (1). Пусть для функции 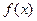выполняются условия:

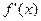1. и 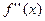непрерывны на ;
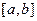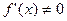2. на .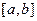

Из условий 1-2 следует непрерывность и строгая монотонность функции 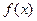на .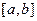

Пусть начальное приближение 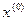принадлежит достаточно малой окрестности корня 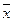уравнения (1). Рассмотрим сначала геометрически процесс получения очередного приближения к решению (рис.1), предусмотренного методом Ньютона.

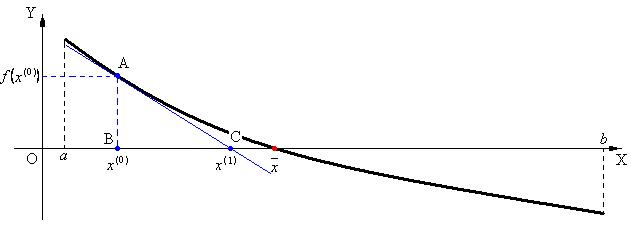
Рис.1.

Через точку 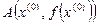проведем касательную к графику функции 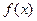. Обозначим точку пересечения касательной с осью ОХ 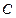, эта точка имеет координаты 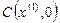; пусть 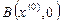(рис.1). Рассмотрим треугольник 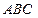. Этот треугольник прямойгольный. В нем: 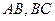- катеты, 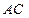- гипотенуза. Тогда:

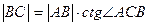, (2)

где - обозначение для длин катетов 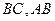соответственно.

Учитывая, что

,

формулу (2) можно записать в виде:

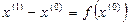
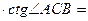
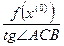. (3)

Очевидно, что

,

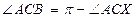а

.

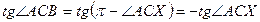Тогда из (3):

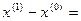
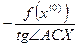. (4)

Угол - это угол, который образует построенная ранее касательная к графику функции 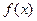в точке 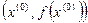с положительным направлением оси ОХ. Вспомним, что из геометрического смысла производной функции в точке следует, что

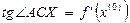. (5)

Подставляя (5) в (4), получаем:

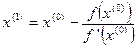. (6)

Формула (6) дает нам новое приближение 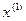к точному решению 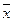уравнения (1). Следующее приближение 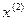получается аналогичным образом из 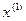и т.д.

Последовательность приближений к точному решению 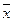уравнения (1) строится по следующей итерационной формуле:

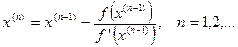(7)

где начальное приближение 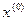должно быть достаточно близко от 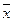. Формула (7) и определяет итерационный процесс метода Ньютона (или метода касательных) решения нелинейного уравнения. Каждая итерация метода связана с получением очередного приближения. Условия 1-2, накладываемые на функцию 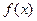, являются обязательными для возможности применения этого метода при решении уравнения (1). Выполнение этих условий в совокупности с обеспечением локализации 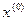в малой окрестности корня 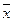обеспечит сходимость метода: получаемая по формуле (7) последовательность приближений 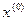, ,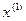..., ,...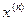. будет стремиться к .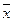