Метод простой итерации решения нелинейного уравнения. Скорость сходимости

Решается нелинейное уравнение (1). Пусть 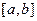содержит единственный корень уравнения (1). Функции 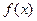определена и непрерывна на .

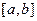Заменим уравнение (1) равносильным ему уравнением:

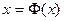. (11)

Выберем произвольно начальное приближение к решению: 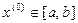. Последующие приближения будем строить по итерационной формуле:

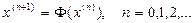(12)

Формула (12) – это итерационная формула метода простой итерации для решения нелинейного уравнения (11).

Теорема. Пусть функция 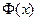определена и дифференцируема на отрезке 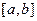, причем значения этой функци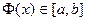и при 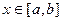. Тогда если существует такое число 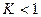, что

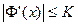при ,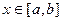

то последовательность приближений 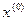, ,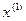..., ,...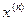., построенная по формуле (12), будет стремиться к единственному корню 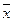уравнения (11) на .

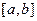Погрешность метода простой итерации на каждом шаге оценивается формулой:

,

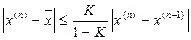откуда вытекает условие окончания счета, т.е. достижения заданной погрешности :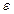

.

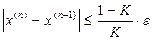Вопросы

1. Общий вид нелинейного уравнения.
2. Геометрический смысл метода Ньютона.
3. Условия, накладываемые на функцию, в методе Ньютона.
4. Вывести итерационную формулу метода Ньютона.
5. Скорость сходимости метода касательных.
6. Недостатки и преимущества метода касательных.
7. Геометрический смысл метода хорд.
8. Условия, накладываемые на функцию, в методе хорд.
9. Вывести итерационную формулу метода хорд.
10. Скорость сходимости метода хорд.
11. Недостатки и преимущества метода хорд.
12. Условия, накладываемые на функцию, в методе простой итерации.
13. Скорость сходимости метода простой итерации.
14. Недостатки и преимущества метода простой итерации.