Скорость сходимости метода Ньютона, преимущества и недостатки

Метод Ньютона является одним из самых быстрых методов решения нелинейного уравнения (имеет большую скорость сходимости). Можно показать, что скорость сходимости метода Ньютона оценивается в соответствии с формулой:

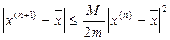, (8)

где 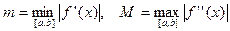. Таким образом, как следует из (8), грубо говоря, каждая итерация возводит ошибку, допущенную на предыдущей итерации, в квадрат. Уменьшение ошибки приближения (в случае сходимости метода Ньютона) от шага к шагу происходит здесь гораздо быстрее, чем в методе деление отрезка пополам.

Однако одним из основных требований сходимости метода Ньютона (и его основным недостатком), как уже отмечалось выше, является локализация начального приближения в достаточно малой окрестности корня уравнения. В противном случае возможна расходимость метода Ньютона (рис.2). Это требование не всегда можно выполнить, т.к. корень не известен. Если в процессе применения метода касательных наблюдается расходимость, то рекомендуется сузить отрезок 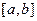и выбрать другое начальное приближение 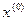. Методу Нютона на практике часто предшествует какой-нибудь гарантированно сходящийся метод (типа метода деления отрезка пополам), и лишь потом происходит переключение на быстро сходящийся метод касательных. Таким образом, мтод Ньютона часто является быстрой завершающей процедурой более медленного гарантированно сходящегося начального алгоритма.

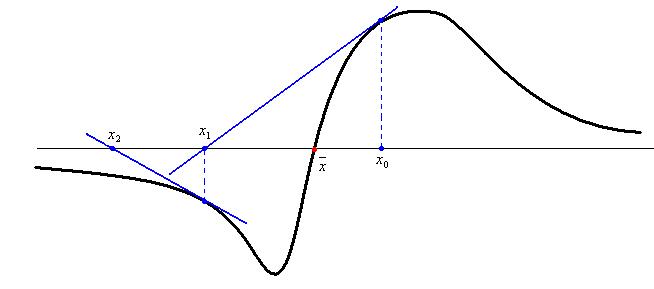
Рис.2.

Еще одним (незначительным) недостатком метода Ньютона является необходимость вычисления производной функции при вычислении очередного приближения к решению (формула (7)). Это не удобно при сложном виде функции .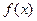

Метод Ньютона можно распространить на решение систем нелинейных уравнений с многими переменными.