Метод хорд решения нелинейного уравнения. Геометрический смысл

Метод хорд (или метод секущих) решения нелинейного уравнения (1) не требует для получения очередного приближения вычисления производной и не настолько, как метод Ньютона, зависит от правильности выбора начальных приближений.

Предположим, что 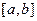содержит единственный корень уравнения (1). Пусть для функции 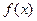выполняются условия:

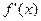1. и 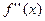непрерывны на ;
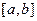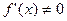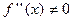2. , на .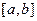

Начальными для метода хорд является не одно, а два приближения к решению: 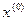, 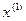. Выясним сначала геометрическое расположение очередного приближения (рис.3). Для его получения в методе хорд через точки графика функции 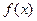с координатами , проводится хорда до пересечения с осью ОХ. Точка пересечения построенной хорды и ОХ и дает следующее приближение 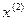к решению уравнения. Для получения аналитического выражения вычисления 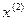рассмотрим два прямоугольных подобных треугольника: 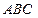и (рис.3). Из подобия треугольников вытекает следующая пропорция:

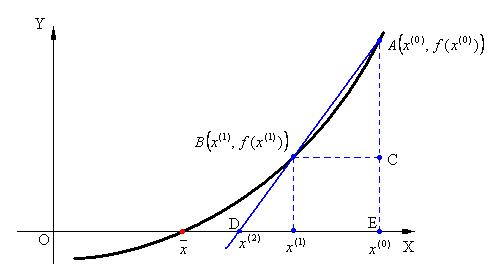
Рис.3.

.

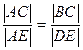Подставляя в эту пропорцию выражения для длин соответствующих сторон треугольников, получим:

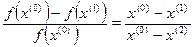. (9)

Разрешая уравнение (9) относительно очередного приближения 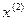к решению, получим:

.

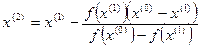Общая итерационная формула метода секущих имеет вид:

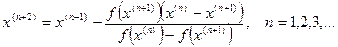
Каждая итерация метода связана с получением очередного приближения к решению уравнения.