Лемма Гершгорина

Лекция 23. Локализация собственных значений

План

Лемма Гершгорина

Понятие инерции матрицы. Связь инерции матрицы и ее свойств

Алгоритм определения количества собственных значений, меньших заданного числа, его преимущества и недостатки

Алгоритм поиска ближайшего к заданному числу собственного значения

Лемма Гершгорина

Определение 1. Локализация собственных значений - определение границ спектра, или границдля каждого собственного значения.

Лемма Гершгорина. Пусть 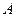- произвольная 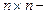матрица. Обозначим

.

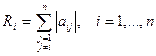Все собственные значения матрицы 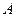находятся в объединении 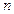кругов с центрами в точках 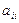и радиусами 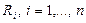, называемых кругами Гершгорина, т.е. для каждого собственного значения 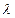матрицы 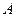обязательно найдется круг, что:

.

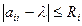Доказательство. Покажем, что каждое собственное значение матрицы 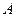попадает хотя бы в один из кругов Гершгорина. Пусть 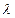- собственное значение матрицы 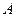, а 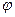- соответствующий собственный вектор, т.е.

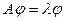. (1)

Обозначим через 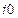индекс такой компоненты вектора 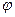, что

.

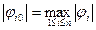Индекс 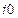может определяться неоднозначно.

Запишем уравнение с номером 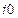из системы (1):

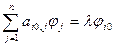. (2)

В левой части равенства (2) выделим слагаемое с номером :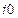

.

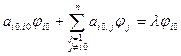Преобразуем эквивалентным образом последнее равенство:

,

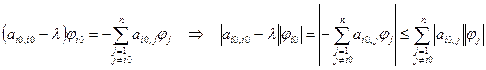Учитывая, что 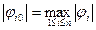, а собственный вектор не может быть нулевым, то 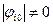, , поэтому последнее неравенство можно разделить почленно на , не меняя знак:

. (3)

Поскольку 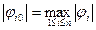, то 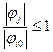, тогда (3) можно продолжить:

,

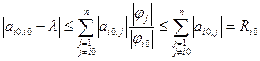что и требовалось доказать.

Следствие. Если все круги Гершгорина, отвечающие матрице 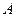попарно не пересекаются, то каждый из них содержит точно одно собственное значение.