Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача 11. Определить коэффициент корреляции между полом и уровнем притязания.
|
|
Определить коэффициент корреляции между полом и уровнем притязания.
| № | |||||||||||
| пол | |||||||||||
| Уровень притязаний |
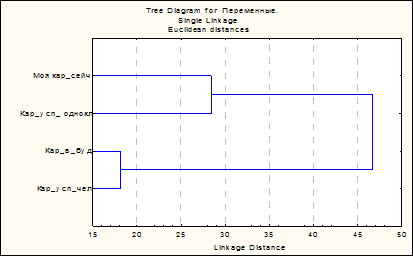
| Сравните дендрограммы - результаты кластерного анализа представлений о карьере | ||||||||||
| старшеклассников | ||||||||||
| 11 класс девочки | ||||||||||
| ||||||||||
| 11 класс мальчики | ||||||||||
| ||||||||||
ЛИТЕРАТУРА
Базовые учебники
1. Наследов А.Д. Математические методы психологического исследования. – СПб: Речь, 2004.
2. Сидоренко Е.В. Методы математической обработки в психологии. - СПб: СПЦ, 1996.
Основная литература
1. Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. – М.: Прогресс, 1976.
2. Гмурман В.Е. Теория вероятностей и математическая статистика. М., 1972
3. Ермолаев О.Ю. Математическая статистика для психологов. – М.: МПСИ, 2002.
4. Наследов А.Д. Многомерные методы математической обработки в психологии. – СПб: СПГУ, 1998.
5. Наследов А.Д. SPSS: Комп’ютерній аналіз данніх в психологи и социальніх науках. – СПб.: Питер, 2005.
6. Мюллер П., Нойман П., Шторм Р. Таблицы по математической статистике. – М., 1982.
7. Суходольский Г.В. Основы математической статистики для психологов. – СПб., 2000.
8. Тарасов С.Г. Основы применения математических методов в психологии. – СПб: СПГУ, 1998.
Дополнительная литература
1. Анастази А. Психологическое тестирование: Книга 2. –М.: Педагогика, 1982. – 382 с.
2. Арестова О. Н., Бабанин Л. Н., Войскунский А.Е. Специфика психологических методов в условиях использования компьютера. – М. 1995.
3. Артемьева Е.Ю., Мартынов Е.М. Вероятностные методы в психологии. – М., 1975.
4. Боровиков В.П. Программа STATISTICA для студентов и инженеров. – М., 2001.
5. Бурлачук Л.Ф., Морозов С.М. Словарь-справочник по психодиагностике. СПб, 1999.
6. Бюль А., Цёфель П. SPSS: искусство обработки информации. – М., СПб, Киев, 2002.
7. Ганзен В.А., Балин В.Д. Теория и методология психологического исследования: Практическое руководство. – СПб.: СПбГУ, 1991.
8. Годфруа Ж. Что такое психология. Том 2. – М., 1996.
9. Головина Г.М., Крылов В.Ю, Савченко Т.Н. Математические методы в современной психологии: статус, разработка, применение. – М. ИП РАН, 1995.
10. Готтсданкер Р. Основы психологического эксперимента. – М.: Академия, 2005. – 368 с.
11. Гудвин Дж. Исследование в психологии: методы и планирование. – СПб: Питер, 2004. – 558 с.
12. Журавлев Г.Е, Структура эксперимента по вероятностному прогнозированию//Вероятностное прогнозирование в деятельности человека. – М.Наука, 1977
13. Исследование в психологии: методы и планирование / Дж.Гудвин. – СПб., 2004. – 558 с.
14. Калинин С.И. Компьютерная обработка данных для психологов. – СПб: Речь, 2002.
15. Куликов Л.В. Введение в психологическое исследование. – СПб., 1994.
16. Немов Р.С. Психология. Книга 3. – М., 1995.
Критические значения выборочного коэффициента корреляции рангов Спирмена (по В.Ю. Урбаху, 1964)
Связь значима, если rэмп > r кр 0, 05, и тем более значима, если rэмп > rкр 0, 01.
| n | p = 5% | p = 1% | n | p = 5% | p = 1% | n | p = 5% | p = 1% |
| 0, 94 | - | 0, 48 | 0, 62 | 0, 37 | 0, 48 | |||
| 0, 85 | - | 0, 47 | 0, 60 | 0, 36 | 0, 47 | |||
| 0, 78 | 0, 94 | 0, 46 | 0, 58 | 0, 36 | 0, 46 | |||
| 0, 72 | 0, 88 | 0, 45 | 0, 57 | 0, 36 | 0, 45 | |||
| 0, 68 | 0, 83 | 0, 44 | 0, 56 | 0, 34 | 0, 45 | |||
| 0, 64 | 0, 79 | 0, 43 | 0, 54 | 0, 34 | 0, 44 | |||
| 0, 61 | 0, 76 | 0, 42 | 0, 53 | 0, 33 | 0, 43 | |||
| 0, 58 | 0, 73 | 0, 41 | 0, 52 | 0, 33 | 0, 43 | |||
| 0, 56 | 0, 70 | 0, 39 | 0, 51 | 0, 33 | 0, 43 | |||
| 0, 54 | 0, 68 | 0, 39 | 0, 50 | 0, 32 | 0, 41 | |||
| 0, 52 | 0, 66 | 0, 38 | 0, 49 | 0, 32 | 0, 41 | |||
| 0, 50 | 0, 64 | 0, 38 | 0, 48 | 0, 31 | 0, 40 |
Критические значения выборочного коэффициента линейной корреляции rs Пирсона (по В.Ю. Урбаху, 1964)
Связь значима, если rэмп > r кр 0, 05, и тем более значима, если rэмп > rкр 0, 01.
| n | p = 5% | p = 1% | n | p = 5% | p = 1% |
| 0, 950 | 0, 990 | 0, 388 | 0, 496 | ||
| 0, 878 | 0, 959 | 0, 384 | 0, 487 | ||
| 0, 811 | 0, 917 | 0, 374 | |||
| 0, 754 | 0, 874 | 0, 367 | 0, 470 | ||
| 0, 707 | 0, 834 | 0, 361 | 0, 463 | ||
| 0, 666 | 0, 798 | 0, 332 | 0, 435 | ||
| 0, 632 | 0, 765 | 0, 310 | 0, 407 | ||
| 0, 602 | 0, 735 | 0, 292 | 0, 384 | ||
| 0, 576 | 0, 708 | 0, 277 | 0, 364 | ||
| 0, 553 | 0, 684 | 0, 253 | 0, 333 | ||
| 0, 532 | 0, 661 | 0, 234 | 0, 308 | ||
| 0, 514 | 0, 641 | 0, 219 | 0, 288 | ||
| 0, 497 | 0, 623 | 0, 206 | 0, 272 | ||
| 0, 482 | 0, 606 | 0, 196 | 0, 258 | ||
| 0, 468 | 0, 590 | 0, 175 | 0, 230 | ||
| 0, 456 | 0, 575 | 0, 160 | 0, 210 | ||
| 0, 444 | 0, 561 | 0, 138 | 0, 182 | ||
| 0, 433 | 0, 549 | 0, 124 | 0, 163 | ||
| 0, 423 | 0, 537 | 0, 113 | 0, 148 | ||
| 0, 413 | 0, 526 | 0, 098 | 0, 128 | ||
| 0, 404 | 0, 515 | 0, 088 | 0, 115 | ||
| 0, 396 | 0, 505 | 0, 062 | 0, 081 |
Квантили t-распределения Стьюдента для доверительной вероятности 1 - a = 0, 95; 0, 99 и 0, 999
Нулевая гипотеза о сходстве принимается при t < t a = 0, 05, и отклоняется при t > t a = 0, 01
| g | 0, 95 | 0, 99 | 0, 999 | g | 0, 95 | 0, 99 | 0, 999 |
| 12, 706 | 63, 657 | 636, 619 | 2, 030 | 2, 724 | 3, 591 | ||
| 4, 303 | 9, 925 | 31, 599 | 2, 021 | 2, 704 | 3, 551 | ||
| 3, 182 | 5, 841 | 12, 924 | 2, 014 | 2, 690 | 3, 520 | ||
| 2, 776 | 4, 604 | 8, 610 | 2, 009 | 2, 678 | 3, 496 | ||
| 2, 571 | 4, 032 | 6, 869 | 2, 004 | 2, 668 | 3, 476 | ||
| 2, 447 | 3, 707 | 5, 959 | 2, 000 | 2, 660 | 3, 460 | ||
| 2, 365 | 3, 450 | 5, 408 | 1, 997 | 2, 654 | 3, 447 | ||
| 2, 306 | 3, 355 | 5, 041 | 1, 994 | 2, 648 | 3, 435 | ||
| 2, 262 | 3, 250 | 4, 781 | 1, 992 | 2, 643 | 3, 426 | ||
| 2, 228 | 3, 169 | 4, 587 | 1, 990 | 2, 639 | 3, 416 | ||
| 2, 201 | 3, 106 | 4, 437 | 1, 988 | 2, 635 | 3, 412 | ||
| 2, 179 | 3, 054 | 4, 318 | 1, 987 | 2, 632 | 3, 402 | ||
| 2, 160 | 3, 012 | 4, 221 | 1, 985 | 2, 629 | 3, 396 | ||
| 2, 145 | 2, 977 | 4, 140 | 1, 984 | 2, 626 | 3, 390 | ||
| 2, 131 | 2, 947 | 4, 073 | 1, 983 | 2, 623 | 3, 386 | ||
| 2, 120 | 2, 921 | 4, 015 | 1, 982 | 2, 621 | 3, 382 | ||
| 2, 110 | 2, 898 | 3, 965 | 1, 980 | 2, 617 | 3, 374 | ||
| 2, 101 | 2, 878 | 3, 922 | 1, 978 | 2, 614 | 3, 366 | ||
| 2, 093 | 2, 861 | 3, 883 | 1, 977 | 2, 611 | 3, 361 | ||
| 2, 086 | 2, 845 | 3, 850 | 1, 976 | 2, 609 | 3, 357 | ||
| 2, 080 | 2, 831 | 3, 819 | 1, 972 | 2, 601 | 3, 340 | ||
| 2, 074 | 2, 819 | 3, 792 | 1, 968 | 2, 592 | 3, 323 | ||
| 2, 069 | 2, 807 | 3, 768 | 1, 966 | 2, 588 | 3, 315 | ||
| 2, 064 | 2, 797 | 3, 745 | 1, 965 | 2, 586 | 3, 310 | ||
| 2, 060 | 2, 787 | 3, 725 | 1, 964 | 2, 584 | 3, 306 | ||
| 2, 056 | 2, 779 | 3, 707 | 1, 9634 | 2, 5829 | 3, 304 | ||
| 2, 052 | 2, 771 | 3, 690 | 1, 9629 | 2, 5820 | 3, 302 | ||
| 2, 048 | 2, 763 | 3, 674 | 1, 9626 | 2, 5813 | 3, 301 | ||
| 2, 045 | 2, 756 | 3, 659 | 1, 9923 | 2, 5808 | 3, 300 | ||
| 2, 042 | 2, 750 | 3, 646 | 1, 9600 | 2, 5758 | 3, 291 |
Квантили Х2 - распределения для доверительной вероятности 1 - a = 0, 95; 0, 99
Нулевая гипотеза о сходстве принимается при Х2 < Хa = 0, 05, и отклоняется при Х2 > Хa = 0, 01
| g | 0, 95 | 0, 99 | g | 0, 95 | 0, 99 | g | 0, 95 | 0, 99 |
| 3, 8415 | 6, 6349 | 50, 9985 | 58, 6192 | 91, 6700 | 101, 6210 | |||
| 5, 9915 | 9, 2103 | 52, 1923 | 59, 8925 | 92, 8080 | 102, 8160 | |||
| 7, 8147 | 11, 3449 | 53, 3835 | 61, 1621 | 93, 9450 | 104, 0100 | |||
| 9, 4877 | 13, 2767 | 54, 5722 | 62, 4281 | 95, 0810 | 105, 2020 | |||
| 11, 0705 | 15, 0863 | 55, 7585 | 63, 6907 | 96, 2170 | 106, 3930 | |||
| 12, 5916 | 16, 8119 | 56, 9424 | 64, 9501 | 97, 3510 | 107, 5820 | |||
| 14, 0671 | 18, 4753 | 58, 1240 | 66, 2062 | 98, 4840 | 108, 7710 | |||
| 15, 5073 | 20, 0902 | 59, 3035 | 67, 4593 | 99, 6170 | 109, 9580 | |||
| 16, 9190 | 21, 6660 | 60, 4809 | 68, 7095 | 100, 7490 | 111, 1440 | |||
| 18, 3070 | 23, 2093 | 61, 6562 | 69, 9568 | 101, 8790 | 112, 3290 | |||
| 19, 6751 | 24, 7250 | 62, 8296 | 71, 2014 | 104, 1390 | 114, 6950 | |||
| 21, 0261 | 26, 2170 | 64, 0011 | 72, 4433 | 105, 2670 | 115, 8760 | |||
| 22, 3620 | 27, 6882 | 65, 1708 | 73, 6826 | 106, 3950 | 117, 0570 | |||
| 23, 6848 | 29, 1412 | 66, 3386 | 74, 9195 | 107, 5220 | 118, 2360 | |||
| 24, 9958 | 30, 5779 | 67, 5050 | 76, 1540 | 108, 6480 | 119, 4140 | |||
| 26, 2962 | 31, 9999 | 68, 6690 | 77, 3860 | 109, 7730 | 120, 5910 | |||
| 27, 5871 | 33, 4087 | 69, 8320 | 78, 6160 | 110, 8980 | 121, 7670 | |||
| 28, 8693 | 34, 8053 | 70, 9930 | 79, 8430 | 112, 0220 | 122, 9420 | |||
| 30, 1435 | 36, 1909 | 72, 1530 | 81, 0690 | 113, 1450 | 124, 1160 | |||
| 31, 4104 | 37, 5662 | 73, 3110 | 82, 2920 | 114, 2680 | 125, 2890 | |||
| 32, 6706 | 38, 9322 | 74, 4680 | 83, 5130 | 115, 3900 | 126, 4620 | |||
| 33, 9244 | 40, 2894 | 75, 6240 | 84, 7330 | 116, 5110 | 127, 6330 | |||
| 35, 1725 | 41, 6384 | 76, 7780 | 85, 9500 | 117, 6320 | 128, 8030 | |||
| 36, 4150 | 42, 9798 | 77, 9310 | 87, 1660 | 118, 7520 | 129, 9730 | |||
| 37, 6525 | 44, 3141 | 79, 0820 | 88, 3790 | 119, 8710 | 131, 1410 | |||
| 38, 8851 | 45, 6417 | 80, 2320 | 89, 5910 | 120, 9900 | 132, 3090 | |||
| 40, 1133 | 46, 9629 | 81, 3810 | 90, 8020 | 122, 1080 | 133, 4760 | |||
| 41, 3371 | 48, 2782 | 82, 5290 | 92, 0100 | 123, 2250 | 134, 6420 | |||
| 42, 5570 | 49, 5879 | 83, 6750 | 93, 2170 | 124, 3420 | 135, 8070 | |||
| 43, 7730 | 50, 8922 | 84, 8210 | 94, 4220 | 135, 0 | ||||
| 44, 9853 | 52, 1914 | 85, 9650 | 95, 6260 | 147, 0 | ||||
| 46, 1943 | 53, 4858 | 87, 1080 | 96, 8280 | 158, 0 | ||||
| 47, 3999 | 54, 7755 | 88, 2500 | 98, 0280 | 169, 0 | ||||
| 48, 6024 | 56, 0609 | 89, 3910 | 99, 2270 | 180, 0 | ||||
| 49, 8018 | 57, 3421 | 90, 6310 | 100, 4250 | 234, 0 | ||||
| 288, 0 |
Критические значения критерия Q Розенбаума для уровней статистической значимости р ≤ 0, 05 и р ≤ 0, 01 (по Гублеру Е.В., Генкину А.А., 1973) Различия между двумя выборками можно считать достоверными (p≤ 0, 05), если Qэмп равен или выше критического значения Q0, 05 и тем более достоверными (р ≤ 0, 01), если Qэмп равен или выше критического значения Q0, 01
| n | ||||||||||||||||
| p=0, 05 | ||||||||||||||||
| 7 | ||||||||||||||||
| p=0, 01 | ||||||||||||||||
Критические значения критерия U Манна-Уитни для уровней статистической значимости р ≤ 0, 05 и р ≤ 0, 01 (по Гублеру Е.В.,
Генкину А.А., 1973) Различия между двумя выборками можно считать значимыми (р ≤ 0, 05), если Uэмп ниже или равен U0, 05 и тем более достоверными (р< 0, 01), если Uэмп ниже или равен U0, 01
| n1 | 7 | ||||||||||||||||||
| n2 | P=0, 05 | ||||||||||||||||||
| - | |||||||||||||||||||
| - | |||||||||||||||||||
| p=0, 01 | |||||||||||||||||||
| - | - | ||||||||||||||||||
| - | - | ||||||||||||||||||
| - | |||||||||||||||||||
| - | |||||||||||||||||||
| - | |||||||||||||||||||
| - | |||||||||||||||||||
| - | |||||||||||||||||||
| - | |||||||||||||||||||
Продолжение
| n1 | ||||||||||||||||||
| n2 | p=0, 05 | |||||||||||||||||