
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача № 12.
|
|
По трубам вертикального теплообменника снизу вверх течет вода. Внутренний диаметр труб d =14 мм; их длина l= 1, 1 м. Расход воды через одну трубу G = 56 кг/ч. Температура воды на входе в теплообменник tж1 = 40 °С.
Определить количество тепла, передаваемого от стенки одной трубы к воде, и температуру воды на выходе, если температура стенок труб поддерживается равной 70 °С.
Решение:
Секундный расход воды: G = 56/3600 = 1, 55∙ 10-2 кг/с
При tж1 = 40 °С вязкость μ ж1 = 653∙ 10-6 Па∙ с
и Reж1 = 4 G / (π d μ ж1) = (4 ∙ 1, 55 ∙ 10-2) / (3, 14∙ 14∙ 10-3∙ 653∙ 10-6) = 2159 < 2300.
Режим течения ламинарный.
Далее необходимо вычислить произведение (GrPr)г. Так как нам неизвестно значение температуры воды на выходе, tж2 и, следовательно, нельзя найти её среднюю температуру, tж, то задачу решаем методом последовательных приближений.
Задаемся tж2 = 60 °С.
Тогда
tж = 0, 5 (tж1+ tж2) = 0, 5(40+60) =50 °С и tг = 0, 5 (tс+ tж) = 0, 5(70+50) = 60 °С.
При этой температуре
β г = 5, 11 ∙ 10-4 К-1; ν г = 0, 478 ∙ 10-6 м2/с; Рrг = 2, 98;
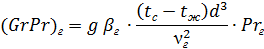
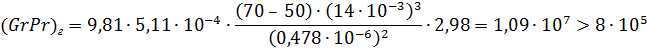
Режим течения вязкостно-гравитационный.
При вязкостно-гравитационном режиме течения в вертикальных трубах и совпадении направлений вынужденной и свободной конвекции у стенки (охлаждение жидкости и течение сверху вниз или нагревание и течение снизу вверх) для расчета средней теплоотдачи можно воспользоваться следующей формулой:
Nuc = 0, 35 (Peг(d/l)0, 3) [(GrPr) г∙ (d/l)]0, 18
где коэффициент теплоотдачи отнесен к начальной разности температур tс - tж;
Индексы «с» и «г» означают, что соответствующие физические свойства выбираются по температуре стенки tс и tг= 0, 5 (tс + tж ).
Формула Nuc = 0, 35 (Peг(d/l)0, 3) [(GrPr)г∙ (d/l)]0, 18 справедлива при Reж < 2300;
(Peг(d/l))ас ≤ Peг(d/l) ≤ 110; 20 ≤ l/d ≤ 130; 8∙ 105 ≤ (GrPr)г ≤ 4∙ 108
Здесь асимптотическое значение числа Пекле:
(Peг (d/l)) ас ≈ 1, 5(GrPr (d/l)) г0, 25
В рассматриваемом случае:
при tг = 60 °С; аг= 1, 6∙ 10-7 м2/с; при tс = 70 °С; λ с = 0, 668 Вт/(м∙ K);
при tж = 50 °С ρ ж = 988 кг/м3.
Средняя скорость течения воды
w = 4 G / (π d2 ρ ж) = 4 ∙ 1, 55∙ 10-2 / (3, 14 ∙ (14∙ 10-2)2 ∙ 988) = 0, 101 м/с
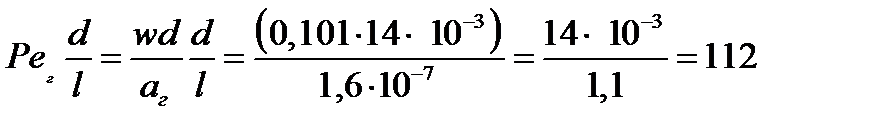
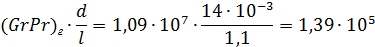
(Peг(d/l))ас ≈ 1, 5(1, 39∙ 105)0, 25 = 29, 17
Так как все критерии находятся в указанных выше пределах, то формула Nuc = 0, 35(Peг(d/l)0, 3) [(GrPr) г∙ (d/l)]0, 18 применима.
Nuc = 0, 35(112)0, 3(1, 39∙ 105)0, 18 = 12, 15.
Коэффициент теплоотдачи
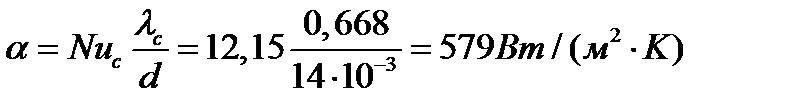
Количество передаваемого тепла
Q = α (tс—tж)π dl = 579(70—50) π 14∙ 10-3 ∙ 1, 1 = 559 Вт.
Проверка принятого значения температуры воды на выходе из трубы:
tж2 = tж1 + (Q/Gcpж) = 40 +(559/(1, 55∙ 10-2 ∙ 4174)) = 40 + 8, 64 = 48, 64 °С
где теплоемкость воды выбрана при tж = 50 °С; срж = 4174 Дж/(кгK).
Таким образом, в результате первого приближения tж2 = 48, 64 °С.
Задавшись для второго приближения tж2 = 50 °С, получим tж = 0, 5 (tж1 + tж2) =45 °С и tг =0, 5 (tс+ tж)= 57, 5 °С. Совпадение достаточно хорошее и дальнейших пересчетов делать не нужно.
Ответ: Q = 559 Вт; tж2 ≈ 49 °С.