
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Структурные средние
|
|
Для расчета степенных средних необходимо располагать информацией не только о значениях признака, но и о величине их весов. При экономическом анализе такая полная информация не всегда доступна. В этом случае предпочтение отдается структурным средним.
Структурные средние позволяют охарактеризовать структуру статистических рядов распределения. К таким показателям относятся мода и медиана.
Модой называется варианта (значение признака), которая наиболее часто встречается в анализируемой совокупности. Наличие двух и более модальных значений может означать неоднородность статистической совокупности.
В дискретном ряду распределения мода (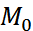 ) — это варианта с максимальной частотой. Например, в табл. 3.5 наибольшей частотой является 88. Этой частоте соответствует модальное значение признака — 37. То есть, наибольшим спросом у покупателей пользуется обувь 37 размера.
) — это варианта с максимальной частотой. Например, в табл. 3.5 наибольшей частотой является 88. Этой частоте соответствует модальное значение признака — 37. То есть, наибольшим спросом у покупателей пользуется обувь 37 размера.
Таблица 3.5 – Дискретный ряд распределения
| Размер обуви | Число купленных пар | Накопленная частота |
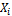
| 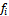
| 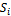
|
| Итого | х |
В интервальном ряду распределения с равными интервалами мода исчисляется по формуле
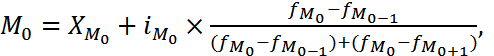 (3.10)
(3.10)
где 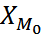 – нижняя граница модального интервала (интервала, имеющего максимальную частоту);
– нижняя граница модального интервала (интервала, имеющего максимальную частоту);
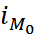 – длина модального интервала;
– длина модального интервала;
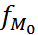 – частота модального интервала;
– частота модального интервала;
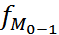 – частота интервала, предшествующего модальному интервалу;
– частота интервала, предшествующего модальному интервалу;
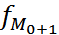 – частота интервала, следующего за модальным интервалом.
– частота интервала, следующего за модальным интервалом.
Определим моду интервального ряда по данным табл. 3.6.
Таблица 3.6 – Интервальный ряд распределения
| Группа предприятий по объему произведенной продукции, млн. руб. | Число предприятий в группе | Накопленная частота |
| 5 – 6, 6 | ||
| 6, 6 – 8, 2 | ||
| 8, 2 – 9, 8 | ||
| 9, 8 – 11, 4 | ||
| 11, 4 – 13, 0 | ||
| 13, 0 – 14, 6 | ||
| Итого | х |
Максимальная частота — 7. Модальным интервалом является интервал (8, 2— 9, 8). В соответствии с формулой (4.10) мода в этом случае
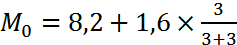 =9, 0 млн. руб.
=9, 0 млн. руб.
Медианой (Ме) называется значение варьирующего признака, которое делит ранжированный ряд данных на две равные части: одна половина единиц анализируемой совокупности будет иметь значение признака меньше медианы, а другая — больше.
При определении Ме по несгруппированным данным сначала их нужно расположить в возрастающем порядке (ранжировать). Затем — определить номер единицы совокупности, значение признака у которой и будет медианой. При небольшом объеме совокупности этот номер определяется визуально, а при большой совокупности — по формуле
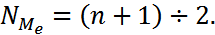 (3.11)
(3.11)
Например, данные о стаже работы семи продавцов представлены в виде ранжированного ряда:
1, 2, 2, 3, 5, 7, 10.
В этом случае 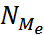 = (7 + 1): 2 = 4. Соответственно,
= (7 + 1): 2 = 4. Соответственно, 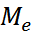 =3 года (четвертая по счету варианта в ранжированном ряду). Если число вариант будет четным: (1, 2, 2, 3, 4, 5, 7, 10),
=3 года (четвертая по счету варианта в ранжированном ряду). Если число вариант будет четным: (1, 2, 2, 3, 4, 5, 7, 10), 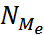 =9: 2=4, 5 и медиана будет равна средней арифметической из 4-й и 5-й варианты: (3 + 4): 2=3, 5 года.
=9: 2=4, 5 и медиана будет равна средней арифметической из 4-й и 5-й варианты: (3 + 4): 2=3, 5 года.
В дискретном ряду распределения (табл. 4.5)
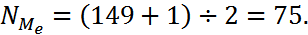 Следовательно,
Следовательно, 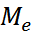 =37.
=37.
Медиана по данным интервального ряда распределения с равными интервалами определяется следующим образом:
1. Для каждого интервала рассчитывается накопленная частота (см. графу 3 табл. 3.6).
2. Определяется медианный интервал. Таким интервалом является тот. накопленная частота которого больше или равна 1/2 численности единиц совокупности. В рассматриваемом примере (табл. 3.6) это будет третий интервал — (8, 2—9, 8). Накопленная частота этого интервала — 14, что больше, чем 12, 5 (половина от объема совокупности).
3. Медиана определяется по формуле
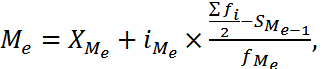 (3.12)
(3.12)
где 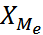 – нижняя граница медианного интервала;
– нижняя граница медианного интервала;
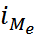 – величина медианного интервала;
– величина медианного интервала;
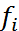 – частота i-го интервала;
– частота i-го интервала;
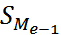 – накопленная частота интервала, предшествующего медианному интервалу;
– накопленная частота интервала, предшествующего медианному интервалу;
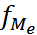 – частота медианного интервала.
– частота медианного интервала.
Расчёт моды и медианы для вариационных рядов с неравными интервалами определяется аналогично, но показатели частоты заменяются показателями абсолютной или относительной плотности распределения, что обеспечивает сопоставимость неравных интервалов. Показатели плотности распределения определяются как отношение частоты к длине интервала:
Средняя арифметическая, мода и медиана являются показателями центра статистического ряда распределения. В каждой конкретной задаче предпочтение может быть отдано любому из этих показателей.
В симметричных рядах распределения величины всех трех показателей совпадают, и предпочтение отдается средней арифметической. Симметричным является распределение, в котором частоты любых двух вариант, равноотстоящих от центра распределения, равны между собой. Для асимметричных рядов предпочтительной характеристикой центра ряда распределения является медиана, поскольку занимает положение между модой и средней арифметической.
В статистическом контроле качества продукции чаще пользуются медианой, а не средней арифметической, поскольку для определения ее в ранжированном ряду не требуется дополнительных расчетов и, кроме того, она не чувствительна к крайним значениям взятой контрольной пробы.
Мода применяется при изучении спроса населения на потребительские товары с целью выявления характеристик продукции, пользующейся повышенным спросом.