Дисперсия альтернативного признака

Признак, для которою существует только два взаимоисключающих варианта значений, называется альтернативным. Например, годная и негодная (бракованная) продукция.

Эквивалентом такого признака можно считать переменную 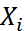, которая принимает значение 1, когда обследуемая единица совокупности обладает изучаемым признаком или 0, когда не обладает.

Обозначим долю единиц, обладающих признаком (годная продукция) — р, а долю единиц, не облагающих признаком (бракованная продукция) – q.

Тогда (р + q)=1

По формуле средней арифметической взвешенной:

r w: val=" 000000" /> < w: sz w: val=" 32" /> < w: sz-cs w: val=" 32" /> < w: lang w: val=" EN-US" /> < /w: rPr> < m: t> X< /m: t> < /m: r> < /m: e> < /m: bar> < /m: oMath> < /m: oMathPara> < /w: p> < w: sectPr wsp: rsidR=" 00000000" > < w: pgSz w: w=" 12240" w: h=" 15840" /> < w: pgMar w: top=" 1134" w: right=" 850" w: bottom=" 1134" w: left=" 1701" w: header=" 720" w: footer=" 720" w: gutter=" 0" /> < w: cols w: space=" 720" /> < /w: sectPr> < /w: body> < /w: wordDocument> "> =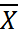

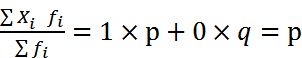
Таким образом, среднее значение альтернативного признака равно частости варианты, обладающей этим признаком.

Дисперсию альтернативного признака рассчитаем по формуле (4.6):

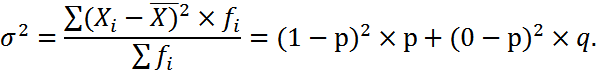
Заменив в этом выражении (1-р) на q, получим

Таким образом, дисперсия альтернативною признака равна произведению доли единиц, обладающих признаком, на долю единиц, не обладающих этим признаком. Предельное значение дисперсии альтернативного признака равно 0, 25, когда p=q=0.5.

Пример. Известно, что качественные товары составили 85% всех отобранных при проверке товаров. Следовательно, на долю бракованных пришлось— 15%.

В соответствии с выше записанными формулами:

r w: val=" 000000" /> < w: sz w: val=" 32" /> < w: sz-cs w: val=" 32" /> < w: lang w: val=" EN-US" /> < /w: rPr> < m: t> X< /m: t> < /m: r> < /m: e> < /m: bar> < /m: oMath> < /m: oMathPara> < /w: p> < w: sectPr wsp: rsidR=" 00000000" > < w: pgSz w: w=" 12240" w: h=" 15840" /> < w: pgMar w: top=" 1134" w: right=" 850" w: bottom=" 1134" w: left=" 1701" w: header=" 720" w: footer=" 720" w: gutter=" 0" /> < w: cols w: space=" 720" /> < /w: sectPr> < /w: body> < /w: wordDocument> "> 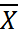=р=85%, а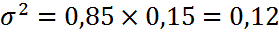

Соответственно среднее квадратическое отклонение определится как

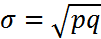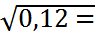= 0, 34.