Показатели вариации. Для измерения вариации (колеблемости) признака в статистике применяются различные абсолютные и относительные показатели:

Для измерения вариации (колеблемости) признака в статистике применяются различные абсолютные и относительные показатели:

1. Размах вариации.

2. Среднее линейное отклонение.

3. Относительное среднее линейное отклонение.

4. Дисперсия.

5. Коэффициент вариации.

Относительными показателями вариации являются коэффициент вариации и относительное среднее линейное отклонение, остальные из перечисленных показателей — абсолютные величины.

Размах вариации определяется как разность между максимальным и минимальным значением изучаемого признака:

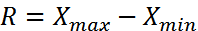(4.1)

Размах вариации является самым простым показателем колеблемости признака. Недостаток его состоит в том, что он показывает отклонение только крайних значений признака и не дает обобщенной характеристики вариации.

Среднее линейное отклонение определяется как средняя арифметическая абсолютных отклонений индивидуальных значений признака от среднего уровня этого признака/

Для несгруппированных данных

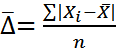. (4.2)

Для сгруппированных данных

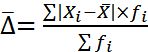. (4.3)

Заметим, что в числителе формул (4.2) и (4.3) представлены суммы абсолютных отклонений без учета знака. Если разности суммировать с учетом знака, числитель этих формул всегда будет равен нулю.

Относительное среднее линейное отклонение определятся как отношение среднего линейного отклонения к средней арифметической, и выражается в процентах:

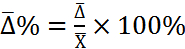. (4.4)

Дисперсия представляет собой среднюю арифметическую из квадратов отклонений индивидуальных значений признака от среднего уровня.

Для несгруппированных данных дисперсия определяется по формуле

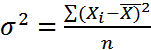. (4.5)

Для сгруппированных данных

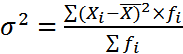. (4.6)

Среднее квадратическое отклонение — квадратный корень из дисперсии.

Для несгруппированных данных

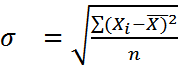. (4.7)

Для сгруппированных данных

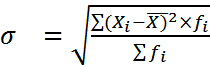. (4.8)

Этот показатель является мерой надежности средней: чем меньше среднее квадратическое отклонение, тем точнее средняя арифметическая отражает средний уровень признака.

Коэффициент вариации определяется по формуле

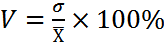. (4.9)

Этот показатель служит относительным измерителем колеблемости признака и однородности совокупности. Если его значение превышает 33%, то совокупность квалифицируют как недостаточно однородную.

Дисперсия и среднее квадратическое отклонение являются наиболее широко применяемыми показателями вариации. Это связано с тем, что они относятся к числу основополагающих показателей теории вероятности и математической статистики, служащих фундаментом теории статистики.

В экономических исследованиях среднее квадратическое отклонение часто используется при определении уровня различных рисков.

Пример. По данным таблицы 4.1 оценим уровень колеблемости стажа рабочих цеха.

Таблица 4.1 – Распределение рабочих цеха по стажу

№	Стаж рабочего	Количество рабочих	Расчетные величины
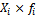
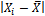
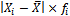
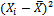
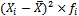
				1, 7	5, 1	2, 89	8, 67
				0, 7	2, 8	0, 49	1, 96
				0, 3	1, 5	0, 09	0, 45
				1, 3	3, 9	1, 69	5, 07
				2, 3	2, 3	5, 29	5, 29
Итого			х	15, 6	х	21, 44

1. Размах вариации:

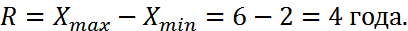
2. Среднее линейное отклонение:

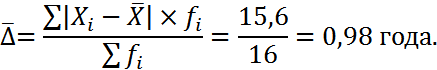
3. Относительное среднее линейное отклонение:

=

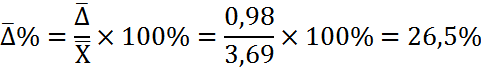
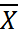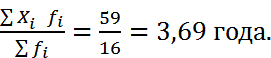
4. Дисперсия:

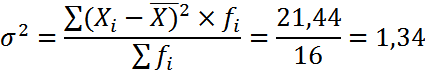
5. Среднее квадратическое отклонение:

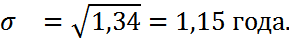
6. Коэффициент вариации.