Теоретические сведения. Все параметры, характеризующие антенны, можно разделить на 2 группы

Все параметры, характеризующие антенны, можно разделить на 2 группы. К первой группе следует отнести параметры, характеризующие антенну как элемент цепи приёмопередающего тракта. Так, передающая антенна может рассматриваться как нагрузка для выходного каскада передатчика и описываться соответствующими параметрами теории цепей: входным сопротивлением, коэффициентом отражения и т. д. Приёмная антенна с этой точки зрения может рассматриваться как обладающий определённым внутренним сопротивлением источник напряжения.

Ко второй группе следует отнести параметры, характеризующие антенну как элемент, преобразующий энергию, поступающую по фидерному тракту, в энергию электромагнитных волн, распространяющихся в пространстве, и распределяющий в пространстве интенсивность полей этих волн (передающая антенна). Приёмная же антенна может рассматриваться как устройство, преобразующее энергию пространственных электромагнитных волн (с учётом направления их прихода) в энергию волн фидера. В эту группу включены такие параметры и характеристики, как коэффициент полезного действия (КПД), диаграмма направленности (ДН), коэффициент направленного действия (КНД), коэффициент усиления (КУ) и др.

Как правило, в реальных антеннах всегда имеются необратимые потери энергии, связанные, в основном, с конечным значением проводимости металла и неидеальностью диэлектрика. Из-за этого мощность , преобразованная антенной, всегда будет меньше мощности 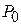, поступающей в антенну. КПД антенны характеризует эффективность преобразования энергии и определяется соотношением .

Другие параметры второй группы, упомянутые здесь, определяются для дальней зоны антенны.

В дальней зоне (зоне излучения) электромагнитное поле, созданное антенной, представляет собой поперечную волну со сферическим волновым фронтом. Дальняя зона формируется при удалении от антенны на расстояние R, удовлетворяющее следующим условиям:

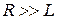, R > > l, , (3.1)

где L – максимальный линейный размер апертуры антенны; l – рабочая длина волны.

ДН описывает пространственное распределение амплитуды поля излучения антенны в дальней зоне.

КНД антенны D характеризует степень концентрации антенного излучения в заданном направлении (обычно в направлении максимального излучения). По определению, значение коэффициента направленного действия показывает, во сколько раз плотность потока мощности излучения рассматриваемой антенны в заданном направлении больше плотности потока мощности, создаваемого изотропным (ненаправленным) излучателем при условии равенства полных мощностей, излучаемых рассматриваемой и изотропной антеннами. Как показано в теории антенн, КНД апертурной антенны с синфазным раскрывом можно найти по формуле

, (3.2)

где 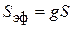– эффективная площадь апертуры; S – её геометрическая площадь; g – апертурный коэффициент использования поверхности раскрыва (КИП), связанный с распределением по апертуре касательной составляющей поля следующим соотношением:

.

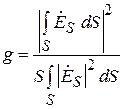КУ антенны G показывает, во сколько раз плотность потока мощности излучения антенны в заданном направлении больше плотности потока мощности, создаваемого идеальным (без потерь) изотропным излучателем при условии равенства мощностей, подводимых к рассматриваемой и изотропной антеннам. Из определения видно, что КУ антенны характеризует степень концентрации излучения в пространстве с учётом потерь в антенне. Между КУ и КНД существует связь: G = D h.

На практике нередко значения КНД или КУ определяют в децибелах (дБ). Коэффициент усиления G 1(в дБ) связан с величиной G, выраженной в относительных единицах, равенством G 1= 10 lg G.

В данной работе производятся измерения коэффициентов усиления рупорных антенн.

Рупорная антенна состоит из отрезка волновода постоянного сечения размером 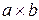и собственно рупора, представляющего собой волновод с плавно изменяющимся сечением, с размерами раскрыва . На практике применяются 2 типа прямоугольных рупоров – секториальные и пирамидальные. Секториальными называются рупоры, у которых расширяется только одна пара стенок. В зависимости от того, в какой плоскости происходит расширение, различают Е -плоскостные (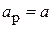, 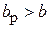) и Н -плоскостные (, 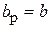) рупоры. Пирамидальными называются рупоры, расширяющиеся как в плоскости вектора Е, так и в плоскости вектора Н.

Характеристики излучения рупорной антенны определяются структурой поля в ее раскрыве. В общем случае ДН плоской прямоугольной излучающей апертуры размером описывается выражением

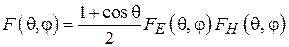. (3.3)

Функции и определяются амплитудно-фазовым распределением поля в раскрыве апертуры в плоскостях векторов E и H соответственно.

Для рупорной антенны с достаточной точностью можно считать, что амплитуда поля в раскрыве распределена так же, как и амплитуда поля основной волны прямоугольного волновода 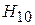, т. е. имеет косинусоидальное распределение вдоль оси x и равномерное вдоль оси y:

.

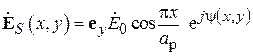В случае синфазного раскрыва (y(x, y) = const) функции и будут определяться формулами

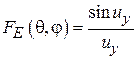, , (3.4)

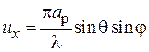, . (3.5)

Значение КИП для синфазной апертуры с таким амплитудным распределением g = 0, 81.

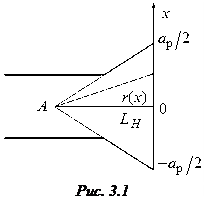Фазовое распределение в апертуре реальной рупорной антенны будет отлично от равномерного. Рассмотрим причину несинфазности раскрыва на примере Н -плоскостного рупора (рис. 3.1). Волна 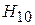питающего волновода, переходя в рупор, трансформируется в волну с цилиндрическим фазовым фронтом, которая как бы исходит из линейного источника A, находящегося на пересечении продолжений граней рупора. Если приближенно считать, что цилиндрическая волна распространяется между параллельными широкими стенками рупора с волновым числом k, то набег фазы в точке апертуры с координатой x равен kr (x), а в центре апертуры – ( – длина Н -плоскостного рупора). Таким образом, разность фаз в точках с координатами x и 0

.

Предполагая, что угол раскрыва рупора мал, заменим корень в этом выражении первыми двумя членами разложения Маклорена:

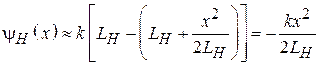. (3.6)

Отсюда видно, что расфазировка возрастает от центра к краю апертуры приблизительно по квадратичному закону и максимальное её значение – фазовая ошибка – достигается на краю раскрыва:

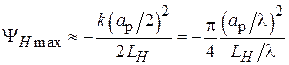. (3.7)

Диаграмма направленности Н -плоскостного рупора с фазовым распределением (3.6) описывается формулой (3.3), где 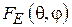определяется выражением (3.4), а при условии малости угла раскрыва рупора даётся интегралом

,

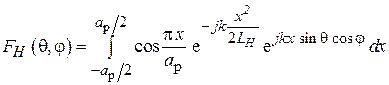который может быть представлен линейной комбинацией специальных функ­ций – интегралов Френеля [6].

На рис. 3.2 представлены диаграммы направленности в плоскости Н (j = 0) для рупора с размером 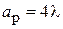при различных значениях нормированной длины рупора 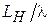и, согласно (3.7), максимальной фазовой ошибки . Кривая 2 соответствует значению 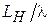= 20, кривая 3 – 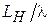= 10, 4 – 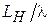= 5. Для сравнения там же приведена диаграмма направленности синфазного раскрыва (кривая 1). Как видно из графиков, наличие в раскрыве квадратичной фазовой ошибки (3.6) приводит к деформации ДН: заплывают нули, увеличивается уровень бокового излучения, расширяется основной лепесток.

Рис. 3.2

Аналогичным образом влияет на диаграмму направленности в плоскости Е (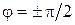) для Е -плоскостного рупора фазовая ошибка , определяемая выражением

.

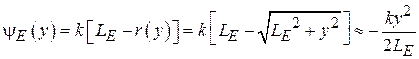В этом случае для расчёта диаграммы направленности рупора в формулу (3.3) следует подставить из (3.5), а 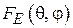будет выражаться интегралом

,

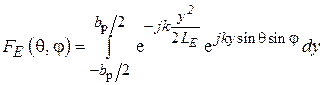также сводимым к линейной комбинации интегралов Френеля.

Влияние фазовой ошибки в раскрыве рупорной антенны проявляется в том, что значение КИП зависит от относительных размеров рупора , , , 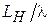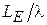. Таким образом, КНД Н -плоскостного рупора будет определяться выражением

,

где 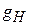– функция, определяющая зависимость КИП (g) от комбинации параметров и 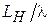. Пользуясь общим выражением для КИП, нетрудно показать, что

.

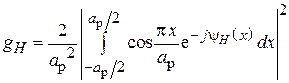Удобнее, однако, иметь дело с приведённым КНД 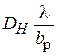, поскольку при варьировании размеров Н -плоскостного рупора отношение остаётся неизменным. Очевидно, приведённый КНД Н -плоскостного рупора будет определяться выражением

.

Аналогичным образом можно найти и приведённый КНД для Е -плос­костного рупора:

,

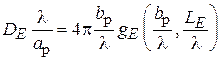где

.

На рис. 3.3 и 3.4 изображены графики зависимостей приведённых КНД 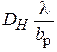и 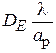от нормированных размеров раскрыва и для H - и E -плоскостных рупоров соответственно. Параметры 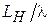на рис. 3.3 и 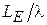на рис. 3.4 принимают значения от 2 (кривая 1) до 6 (кривая 11) с шагом 0, 4. Как видно из этих графиков, с увеличением относительных размеров раскрыва рупора ( или ) при его неизменной длине КНД сначала возрастает, так как увеличиваются размеры излучающей поверхности, которая остаётся практически синфазной (сдвиг фаз 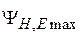мал). При этом ДН становится уже. При дальнейшем увеличении размеров раскрыва заметно растут фазовые искажения, что приводит к снижению КНД и расширению ДН.

Рис. 3.3

Допустимое значение максимальной фазовой ошибки 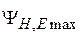определяется условием получения наибольшего КНД при заданной относительной длине рупора. Установлено, что в случае Е -плоскостного рупора максимальный КНД получается при выполнении соотношения , что

Рис. 3.4

соответствует максимальной допустимой фазовой ошибке 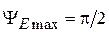. Оптимальная длина и максимальная допустимая фазовая ошибка Н -плоско­стного рупора определяются, соответственно, выражениями и .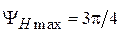

Увеличение допустимого сдвига фаз в апертуре Н -плоскостного рупора по сравнению с Е -плоскостным объясняется спаданием амплитуды возбуждающего поля к краям этого рупора.

Следует отметить, что «оптимальность» здесь понимается в смысле получения наибольшего значения КНД при заданной длине рупора или .

Коэффициент направленного действия оптимального Е - или Н -плоско­стного рупора

.

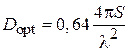КНД пирамидального рупора с размерами раскрыва и можно рассчитать по формуле

, (3.8)

где приведённые значения КНД для секториальных рупоров 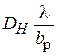и могут быть определены по графикам на рис. 3.3 и 3.4.