
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лекция 5. Двумерные и многомерные случайные величины
|
|
Двумерная СВ, совместная функция распределения и ее свойства. Дискретная двумерная СВ. Непрерывная двумерная СВ. Независимые случайные величины. Ковариация и коэффициент корреляции СВ, их свойства. Условное математическое ожидание. Регрессия.
ОЛ-1 гл 5, 7, 8.
Определение. Совокупность случайных величин X 1 = X 1(ω),.... Хп = Хn (ω), заданных на одном и той же вероятностном пространстве (Ω, B, Р), называют многомерной (n-мерной) случайной величиной, или n-мерным случайным вектором. При этом сами случайные величины Х 1, Х 2,..., Хп называют координатами случайного вектора. В частности, при n = 1 говорят об одномерной, при n = 2 − двумерной случайной величине (или двумерном случайном векторе).
Пример. Отклонение точки разрыва снаряда от точки прицеливания при стрельбе по плоской цели можно задать двумерной случайной величиной (X, Y), где X − отклонение по дальности, а Y − отклонение в боковом направлении.
Определение. Функцией распределения (вероятностей)
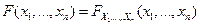
(n -мерного) случайного вектора 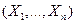 называют функцию, значение которой в точке
называют функцию, значение которой в точке 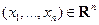 равно вероятности совместного осуществления (пересечения) событий { X 1 < x 1},..., { Xn < xn }, т.е.
равно вероятности совместного осуществления (пересечения) событий { X 1 < x 1},..., { Xn < xn }, т.е. 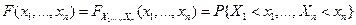
Функцию распределения 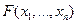 называют также совместной (n-мерной) функцией распределения случайных величин Х 1, Х 2,..., Хп.
называют также совместной (n-мерной) функцией распределения случайных величин Х 1, Х 2,..., Хп.
Теорема. Двумерная функция распределения удовлетворяет следующим свойствам.
1. 0 ≤ F (x 1, x 2) ≤ 1.
2. F (x 1, x 2) − неубывающая функция по каждому из аргументов х 1и х 2.
3. 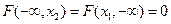 .
.
4. 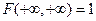 .
.
5. 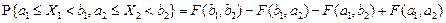 .
.
6. F (x 1, x 2) − непрерывная слева в любой точке 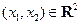 по каждому из аргументов x 1и x 2 функция.
по каждому из аргументов x 1и x 2 функция.
7. 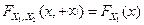 ,
, 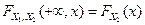 .
.
Доказательство. Утверждения 1 и 2 доказываются точно так же, как и в одномерном случае. 3. События { Х 1 < − ∞ } и { Х 2 < − ∞ } являются невозможными, а пересечение невозможного события с любым событием, как известно, также невозможное событие, вероятность которого равна нулю. Отсюда с учетом определения вытекает утверждение 3.
Аналогично из того, что события { Х 1 < +∞ } и { Х 2 < +∞ } так же, как и их пересечение, являются достоверными, вероятность которых равна единице, вытекает утверждение 4.
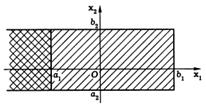 Чтобы найти вероятность попадания двумерной случайной величины (Х 1, Х 2)в прямоугольник Чтобы найти вероятность попадания двумерной случайной величины (Х 1, Х 2)в прямоугольник 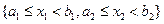 (на рис. заштрихован), сначала определим вероятность попадания в полуполосу (на рис. заштрихован), сначала определим вероятность попадания в полуполосу 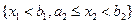 (отмечена двойной штриховкой). Но эта вероятность представляет собой вероятность попадания в квадрант (отмечена двойной штриховкой). Но эта вероятность представляет собой вероятность попадания в квадрант 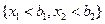 за вычетом вероятности попадания в квадрант за вычетом вероятности попадания в квадрант 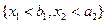 т.е. т.е. 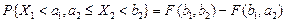 Теперь осталось заметить, что вероятность попадания в прямоугольник
Теперь осталось заметить, что вероятность попадания в прямоугольник 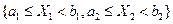 совпадает с вероятностью попадания в полуполосу совпадает с вероятностью попадания в полуполосу 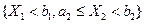 , из которой вычитается вероятность попадания в полуполосу , из которой вычитается вероятность попадания в полуполосу 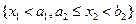 , равная , равная 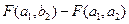 . Окончательно получим утверждение 5.
Подобно одномерному случаю доказывается и утверждение 6. Наконец, событие { Х 2 < +∞ } является достоверным, поэтому . Окончательно получим утверждение 5.
Подобно одномерному случаю доказывается и утверждение 6. Наконец, событие { Х 2 < +∞ } является достоверным, поэтому
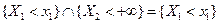 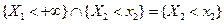
|
Утверждение 7 устанавливает естественную связь между двумерной функцией распределения 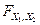 случайного вектора (Х 1, Х 2)и функциями
случайного вектора (Х 1, Х 2)и функциями 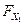 и
и 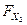 , которые называют одномерными (говорят также частными, или маргинальными) функциями распределения случайных величин X 1и Х 2.
, которые называют одномерными (говорят также частными, или маргинальными) функциями распределения случайных величин X 1и Х 2.