
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Непрерывные случайные величины
|
|
Определение. Непрерывной двумерной случайной величиной (X, Y)называют такую двумерную случайную величину (X, Y), совместную функцию распределения которой можно представить в виде сходящегося несобственного интеграла:
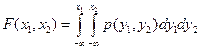
Функцию 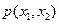 называют совместной двумерной плотностью распределения случайных величин X и Y, или плотностью распределения случайного вектора (X, Y).
называют совместной двумерной плотностью распределения случайных величин X и Y, или плотностью распределения случайного вектора (X, Y).
Так же как и в одномерном случае, будем предполагать, что 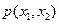 непрерывная (или непрерывная за исключением отдельных точек или линий) функция по обоим аргументам. Тогда в соответствии с определением непрерывной случайной величины и теоремой о дифференцировании интеграла с переменным верхним пределом совместная плотность распределения представляет собой (в точках ее непрерывности) вторую смешанную производную совместной функции распределения:
непрерывная (или непрерывная за исключением отдельных точек или линий) функция по обоим аргументам. Тогда в соответствии с определением непрерывной случайной величины и теоремой о дифференцировании интеграла с переменным верхним пределом совместная плотность распределения представляет собой (в точках ее непрерывности) вторую смешанную производную совместной функции распределения:
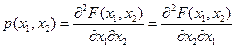
Теорема. Двумерная плотность распределения обладает следующими свойствами:
l) 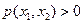 2)
2) 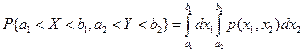
3) 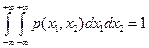
4) 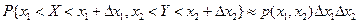
5) 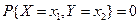 ; 6)
; 6) 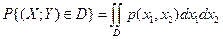
7) 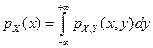 ; 8)
; 8) 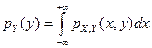
Доказательство. Свойства 1− 5 аналогичны свойствам одномерной плотности распределения. Свойство 6 является обобщением свойства 2.
Докажем утверждения 7 и 8. Из свойства 7 двумерной функции распределения и определения двумерной плотности распределения вытекает:
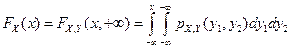
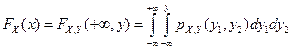 откуда, дифференцируя интегралы по переменному верхнему пределу, получаем утверждение 7 для одномерных (частных, маргинальных) плотностей распределения рX (х)и pY (y)случайных величин X и Y.
откуда, дифференцируя интегралы по переменному верхнему пределу, получаем утверждение 7 для одномерных (частных, маргинальных) плотностей распределения рX (х)и pY (y)случайных величин X и Y.
|
Определение. Случайные величины X и Y называют независимыми, если совместная функция распределения FX, Y (х, у)является произведением одномерных функций распределения FX (x)и FY (y): FX, Y (х, у) = FX (x) FY (y). В противном случае случайные величины называют зависимыми.
Теорема. Для того чтобы непрерывные случайные величины X и Y были независимыми, необходимо и достаточно, чтобы для всех х и у pX, Y (х, у) = pX (x) pY (y).
Доказательство. Пусть случайные величины X и Y независимые. Тогда, согласно определению, FX, Y (х, у) = FX (x) FY (y). С учетом свойств совместной плотности распределения имеем
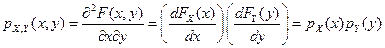 Тем самым необходимость утверждения доказана.
Для доказательства достаточности следует воспользоваться определением двумерной плотности распределения и определением независимости случайных величин
Тем самым необходимость утверждения доказана.
Для доказательства достаточности следует воспользоваться определением двумерной плотности распределения и определением независимости случайных величин
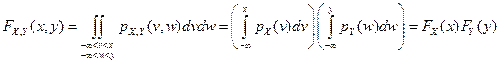
|
Теорема. Дискретные случайные величины X и Y являются независимыми тогда и только тогда, когда для всех возможных значений xi и yi:
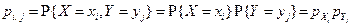
Определение. Ковариацией (корреляционным моментом)cov(X 1, X 2) случайных величин X 1и X 2называют математическое ожидание произведения случайных величин 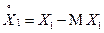 и
и 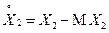
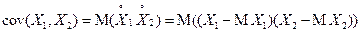
Для дискретных случайных величин X 1и X 2
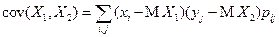
для непрерывных случайных величин X 1и X 2
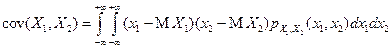
Полезное равенство для произвольных случайных величин
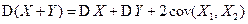
Теорема. Ковариация имеет следующие свойства.
1. cov(X, X) = D X.
2. cov(X 1, X 2)= 0 для независимых случайных величин X 1и X 2.
3. Если Y 1 = a 1 X 1 + b 1и Y 2 = a 2 X 2 + b 2, то cov(Y 1, Y 2) = a 1 a 2cov(X 1, X 2).
4. 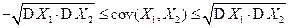 .
.
5. Равенство 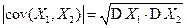 верно тогда и только тогда, когда случайные величины X 1и X 2связаны линейной зависимостью, т.е. существуют такие числа a и b, при которых X 2 = aX 1 + b.
верно тогда и только тогда, когда случайные величины X 1и X 2связаны линейной зависимостью, т.е. существуют такие числа a и b, при которых X 2 = aX 1 + b.
6. cov(X 1, X 2) = M(X 1 X 2) − M X 1M X 2.
Доказательство. 1) Утверждение вытекает из очевидного соотношения cov(X, X) = М(Х − M X)2.
2) Если случайные величины Х 1и Х 2являются независимыми (и имеют математические ожидания), то
cov(X 1, X 2) = M((X 1 − М Х 1)(Х 2− М Х 2))= (M(X 1 − М Х 1))(M(Х 2− М Х 2)),
откуда приходим к утверждению 2.
3) Пусть Y = a 1 X 1 + b, Y 2 = a 2 X 2 + b 2. Тогда
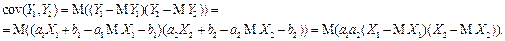 4) Рассмотрим дисперсию случайной величины Yx = xX 1 − X 2, где х − произвольное число. В силу свойств дисперсии и свойства 3 ковариации
4) Рассмотрим дисперсию случайной величины Yx = xX 1 − X 2, где х − произвольное число. В силу свойств дисперсии и свойства 3 ковариации
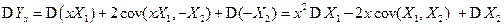 Дисперсия D Yx, как функции от х, представляет собой квадратный трехчлен. Но дисперсия любой случайной величины не может быть меньше нуля, а это означает, что дискриминант D = (2 cov(X 1, X 2))2 − 4 D X 1D X 2 квадратного трехчлена D Yx является неположительным.
5) Пусть выполнено равенство
Дисперсия D Yx, как функции от х, представляет собой квадратный трехчлен. Но дисперсия любой случайной величины не может быть меньше нуля, а это означает, что дискриминант D = (2 cov(X 1, X 2))2 − 4 D X 1D X 2 квадратного трехчлена D Yx является неположительным.
5) Пусть выполнено равенство 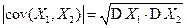 . Значит, дискриминант D равен нулю, и уравнение D Yx = 0 имеет решение, которое обозначим а. Тогда случайная величина Ya = аХ 1 − X 2принимает всего одно значение (допустим, b), и, следовательно,
Х 2 = аХ 1 − b, т.е. случайные величины X 1и X 2связаны линейной зависимостью.
Наоборот, пусть X 2 = aX 1 + b. Тогда в соответствии со свойством 1 дисперсии D Ya = 0, а значит, дискриминант D является неотрицательным. Поскольку при доказательстве утверждения 4 было показано, что этот дискриминант неположителен, то он равен нулю, откуда следует, что . Значит, дискриминант D равен нулю, и уравнение D Yx = 0 имеет решение, которое обозначим а. Тогда случайная величина Ya = аХ 1 − X 2принимает всего одно значение (допустим, b), и, следовательно,
Х 2 = аХ 1 − b, т.е. случайные величины X 1и X 2связаны линейной зависимостью.
Наоборот, пусть X 2 = aX 1 + b. Тогда в соответствии со свойством 1 дисперсии D Ya = 0, а значит, дискриминант D является неотрицательным. Поскольку при доказательстве утверждения 4 было показано, что этот дискриминант неположителен, то он равен нулю, откуда следует, что
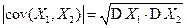 6) Раскрывая скобки в формуле, определяющей ковариацию, и используя свойства математического ожидания, получаем требуемое.
6) Раскрывая скобки в формуле, определяющей ковариацию, и используя свойства математического ожидания, получаем требуемое.
|
Определение. Случайные величины X и Y называют некоррелированными, если их ковариация равна нулю, т.е. cov(Х, Y) = 0.
Определение. Коэффициентом корреляции случайных величин X и Y называют число ρ = ρ (X, Y), определяемое равенством (предполагается, что D X > 0 и D Y > 0)
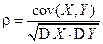
Теорема. Коэффициент корреляции имеет следующие свойства.
1. ρ (X, X) = 1.
2. Если случайные величины X и Y являются независимыми (и существуют D X > 0 и D Y > 0), то ρ (X, Y)= 0.
3. ρ (a 1 X 1 + b 1, a 2 X 2 + b 2) = ± ρ (X 1, X 2)При этом знак плюс нужно брать в том случае, когда а 1и а 2имеют одинаковые знаки, и минус − в противном случае.
4. − 1 ≤ ρ (X, Y) ≤ 1.
5. |ρ (X, Y)| = 1 тогда и только тогда, когда случайные величины X и Y связаны линейной зависимостью.