
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Условные распределения
|
|
В случае дискретной СВ закон распределения двумерного случайного вектора (X, Y)удобно задавать набором вероятностей pij = P{ X = xi, Y = y j} для всех значений i и j. Зная вероятности pij, нетрудно найти законы распределений каждой из координат по формулам
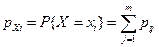 ,
, 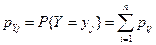
Определение. Для двумерной дискретной случайной величины(X, Y) условной вероятностью π ij, i = 1,..., n, j = 1,..., m, того, что случайная величина X примет значение xi при условии Y = yj, называют условную вероятность события { X = xi }при условии события { Y = yj } т.е.
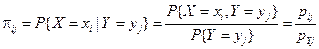
При каждом j, j = 1,..., m, набор вероятностей π ij, i = 1,..., n, определяет, с какими вероятностями случайная величина X принимает различные значения хi, если известно, что случайная величина Y приняла значение yj. Иными словами, набор вероятностей π ij, i = 1,..., n, характеризует условное распределение дискретной случайной величины X при условии Y = уj.
Аналогично определяют условную вероятность  того, что случайная величина Y примет значение yj при условии X = хi.
того, что случайная величина Y примет значение yj при условии X = хi.
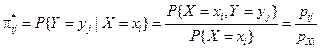
| X 1 | X 2 | ||
| PX 1 | |||
| q | q | q | |
| p | p | p | |
| P X 2 | q | p |
Пример 1. Условное распределение числа Х 1успехов в первом испытании по схеме Бернулли при условии, что число успехов во втором испытании X 2 = j, j = 0, 1, задается таблицей. Из этой таблицы следует, что, независимо от числа успехов во втором испытании, 0 или 1 успех в первом испытании происходит с одними и теми же вероятностями р и q. Это очевидно, поскольку испытания по схеме Бернулли являются независимыми.
Пример 2. Условное распределение случайной величины X (числа очков, выпавших на верхней грани игральной кости) при условии Y = yj (числа очков, выпавших на нижней грани игральной кости), j = 1,..., 6, представлено в таблице. Действительно, если, например, на нижней грани выпало одно очко, то на верхней грани может выпасть только шесть очков (π 61 = 1).
| X | Y | ||||||
| Р X | |||||||
| 1/6 | |||||||
| 1/6 | |||||||
| 1/6 | |||||||
| 1/6 | |||||||
| 1/6 | |||||||
| 1/6 | |||||||
| P Y | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Перейдем к случаю, когда двумерный случайный вектор (X, Y) имеет непрерывную совместную плотность распределения р (х, у) и непрерывные маргинальные плотности распределения
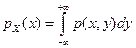 ,
, 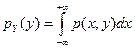
Условная функция распределения
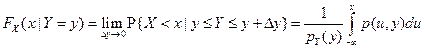
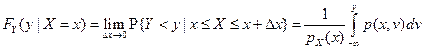
Определение. Условной плотностью распределения случайной величины X (случайной величины Y), являющейся координатой двумерного случайного вектора (X, Y), при условии, что другая его координата приняла некоторое фиксированное значение у (значение x), т.е. Y = y (X = x), называют функцию рX (x|у)(рY (y|x)) определяемую соотношением
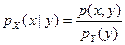
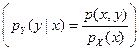
Критерий независимости случайных величин X и Y. Случайные величины X и Y являются независимыми тогда и только тогда, когда условное распределение (функция распределения, плотность распределения) случайной величины X при условии Y = у совпадает с безусловным распределением (функцией распределения, плотностью распределения) случайной величины X.
Определение. Для дискретной двумерной случайной величины (X, Y) значением М(Х | Y = yj) условного математического ожидания дискретной случайной величины X при условии Y = yj, называют число
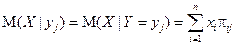
Определение. Условным математическим ожиданием М(Х|Y)дискретной случайной величины X относительно дискретной случайной величины Y называют функцию M(X | Y) = g (Y) от случайной величины Y, где область определения функции g (у)совпадает с множеством значений y 1,..., ym случайной величины Y, а каждому значению yj аргумента у поставлено в соответствие число g (уj) = М(Х | уj).
Подчеркнем еще раз, что условное математическое ожидание М(X | Y) является функцией от случайной величины, т.е. также случайной величиной.
Пример 3. Найдем условное математическое ожидание М(Х | Y) случайной величины X − числа очков, выпавших на верхней грани игральной кости, относительно случайной величины Y − числа очков, выпавших на нижней грани (см. пример 2). В соответствии с таблицей
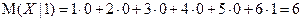
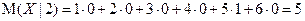
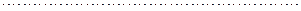
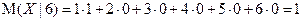
Полученный результат в терминах условного математического ожидания можно записать в виде М(Х |Y) = 7 − Y.
Теорема. Условное математическое ожидание M(Х|Y)обладает следующими свойствами.
1. М(с | Y) = с.
2. M(aX + b|Y) = a M(X|Y) + b.
3. M(X 1 + X 2 |Y) = M(X 1 |Y) + M(X 2 |Y).
4. Пусть случайные величины Х 1и Х 2являются независимыми при условии, что случайная величина Y приняла любое конкретное значение. Тогда M (X 1 X 2 |Y) = M(X 1 |Y)M(X 2| Y).
5. M X = M(M(X|Y)).
6. Пусть и (Х)и v (Y) − функции от случайных величин X и Y. Тогда M(u (X) v (Y) |Y) = v (Y)M(u (X) |Y).
7. Если X и Y − независимые случайные величины, то М(X|Y)= M X.
Определение. Для непрерывной двумерной случайной величины (X, Y) значением М(Х|у) = M(Х|Y = y) условного математического ожидания непрерывной случайной величины X при условии Y = у называют число
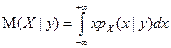
Определение. Для непрерывной двумерной случайной величины (X, Y) условным математическим ожиданием M(X|Y)непрерывной случайной величины X относительно случайной величины Y называют функцию g (Y)= М(Х | Y) от случайной величины Y, принимающую значение g (у)= М(X | у) при Y = у.
Определение. Функцию g (у)называют функцией регрессии, или просто регрессией, случайной величины X на случайную величину Y, а ее график − линией регрессии случайной величины X на случайную величину Y, или просто X на Y.
Линия регрессии графически изображает зависимость „в среднем" случайной величины X от значения случайной величины Y.
Закон больших чисел и центральная предельная теорема
С самого начала изучения курса теории вероятностей мы говорили о том, что практическое применение методов этой математической дисциплины основывается на законе предельного постоянства частоты события.
Закон предельного постоянства частоты события установлен эмпирически. В соответствии с этим законом повторение одного и того же опыта приводит к тому, что частота появления конкретного случайного события теряет свойства случайности и приближается к некоторому пределу, который в соответствии со статистическим определением вероятности и называют вероятностью.
Однако для того чтобы теория согласовывалась с практикой, при аксиоматическом определении вероятности, которое мы использовали, этот закон предельного постоянства частоты должен быть обоснован теоретически. Иначе говоря, он должен быть сформулирован и доказан в виде одной или нескольких теорем. В теории вероятностей теоремы такого типа обычно называют различными формами закона больших чисел, которые, в частности, поясняют смысл математического ожидания случайной величины, и то, почему его называют также средним значением. Центральная предельная теорема, в свою очередь, объясняет то широкое распространение, которое получило на практике нормальное распределение.
Определение. Последовательность Х 1, Х 2,..., Xn,... случайных величин удовлетворяет закону больших чисел (слабому), если для любого ε > 0
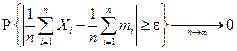 Иными словами, выполнение закона больших чисел отражает предельную устойчивость средних арифметических случайных величин: при большом числе испытаний они практически перестают быть случайными и совпадают со своими средними значениями.
Теорема. Если последовательность Х 1, Х 2,..., Xn,... независимых случайных величин такова, что существуют M Xi = mi и D Xi = σ i, причем дисперсии
Иными словами, выполнение закона больших чисел отражает предельную устойчивость средних арифметических случайных величин: при большом числе испытаний они практически перестают быть случайными и совпадают со своими средними значениями.
Теорема. Если последовательность Х 1, Х 2,..., Xn,... независимых случайных величин такова, что существуют M Xi = mi и D Xi = σ i, причем дисперсии 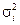 ограничены в совокупности (т.е. ограничены в совокупности (т.е. 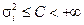 ), то для последовательности Х 1, Х 2,..., Xn,... выполнен закон больших чисел.
При этом говорят также, что к последовательности Х 1, Х 2,..., Xn,... случайных величин применим закон больших чисел в форме Чебышева. ), то для последовательности Х 1, Х 2,..., Xn,... выполнен закон больших чисел.
При этом говорят также, что к последовательности Х 1, Х 2,..., Xn,... случайных величин применим закон больших чисел в форме Чебышева.
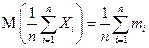 , , 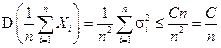
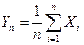 , , 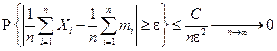 Следствие. Если случайные величины Хi, i = 1, 2,..., в условиях предыдущей теоремы являются также одинаково распределенными (в этом случае mi = m и
Следствие. Если случайные величины Хi, i = 1, 2,..., в условиях предыдущей теоремы являются также одинаково распределенными (в этом случае mi = m и 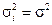 ), то последовательность Х 1, Х 2,..., Xn,... случайных величин удовлетворяет закону больших чисел в следующей форме: ), то последовательность Х 1, Х 2,..., Xn,... случайных величин удовлетворяет закону больших чисел в следующей форме:
 Теорема. (центральная предельная теорема). Пусть X 1, X 2,..., Xn,... − последовательность независимых одинаково распределенных случайных величин, M Xn = m, D Xn = σ 2. Тогда
Теорема. (центральная предельная теорема). Пусть X 1, X 2,..., Xn,... − последовательность независимых одинаково распределенных случайных величин, M Xn = m, D Xn = σ 2. Тогда
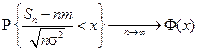 где Ф(х) − функция стандартного нормального распределения.
где Ф(х) − функция стандартного нормального распределения.
|