Дискретные двумерные случайные величины

Определение. Двумерную случайную величину (X, Y) называют дискретной, если каждая из случайных величин X и Y является дискретной.

Как и в одномерном случае, распределение двумерной дискретной случайной величины естественно описать с помощью перечисления всевозможных пар (x_i, y_i) значений координат случайного вектора (X, Y) и соответствующих вероятностей, с которыми эти пары значений принимают случайные величины X и Y.

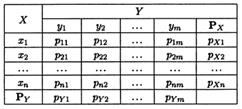
Для простоты ограничимся конечным множеством возможных значений, когда случайная величина X может принимать только значения х ₁, ..., х_п, Y − значения y ₁, ..., y_п. Такое перечисление удобно представить в виде таблицы.

Используя табл., нетрудно определить совместную функцию распределения F_{X, Y} (x, y). Ясно, что для этого необходимо просуммировать р_ij по всем тем значениям i и j, для которых x_i < х, y_j < у, т.е.

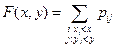
Пример. В соответствии со схемой Бернулли с вероятностью успеха р и вероятностью неудачи q = 1 − р проводятся два испытания. Выпишем распределение двумерного случайного вектора (X ₁, Х ₂), где X_i, i = 1, 2, − число успехов в i -м испытании. Каждая из случайных величин Х ₁и Х ₂может принимать два значения: 0 или 1.