Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание 1
|
|
Выполнение этого задания предполагает знание алгоритма геометрического решения задач линейного программирования.
Типовой пример:
Построить на плоскости область решений системы линейных неравенств
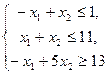
и геометрически найти наименьшее и наибольшее значения линейной функции f = 2 x 1 + 4 x 2 в этой области.
Решение:
Построим множество решений системы неравенств:
1) 
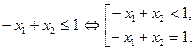
а)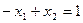 
– прямая l 1, проходящая через точки (0; 1) и (-1; 0);
б) точка (0; 0) удовлетворяет неравенству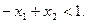 
Таким образом, решением первого неравенства системы ограничений являются точки прямой l 1: 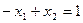и полуплоскости, содержащей начало координат (0; 0).
2) 
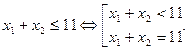
а)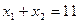 
– прямая, проходящая через точки (0; 11) и (11; 0);
б) точка (0; 0) удовлетворяет неравенству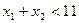 
, т.е. решением второго неравенства являются точки прямой l 2: 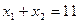и полуплоскости, содержащей начало координат (0; 0).
3) 
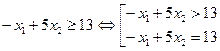
а)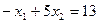 
– прямая l 3, проходящая через точки (2; 3) и
(- 3; 2);
б) точка (0; 0) не удовлетворяет неравенству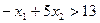 
, значит решением третьего неравенства системы ограничений являются точки прямой l 3: 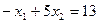и точки полуплоскости, не содержащей начало координат (0; 0).
Решением системы ограничений является треугольник АВС, внутри которого пересекаются решения всех неравенств системы (рис.1).
x1
 
11 -
10 -
 9 -
8 -
7 - B
  6 - •
5 -
4 - A •
l3 l3 3 - • C
    • 2 -
1 -
  ׀ ׀ ׀ 0 ׀ ׀ ׀ ׀ ׀ ׀ ׀ ׀ ׀ ׀ ׀ ׀ ׀ ׀ ׀ ׀ x2
-3 -2 -1 1 2 3 4 5 6 7 8 9 10 11
l1 l1 l2
|
Рис. 1. Множество допустимых решений системы ограничений
Чтобы найти наименьшее и наибольшее значения целевой функции f = 2х1 + 4х2 положим f = 0, тогда 2х1 + 4х2 = 0 – прямая, проходящая через точки (0; 0) и (2; -1).
Градиент целевой функции – вектор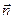 
(2; 4) (начало вектора 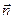лежит в точке (0; 0), а конец в точке, координаты которой равны коэффициентам перед переменными в выражении функции f).
Перемещая прямую f = 0 в направлении вектора 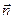видим, что наименьшее значение целевая функция f = 2х1 + 4х2 имеет в точке А, а наибольшее в точке В (рис. 2).
 x1
11 -
 10 -
9 -
8 -
7 - B
 6 - max
5 -
  4 - A
 3 -
l3 2 - min C
1 -
    0
   -3 2 1 1 2 3 4 5 6 7 8 9 10 11 x2
 l2
l1 f=0
|
Рис. 2. Наименьшее и наибольшее значения функции f = 2х1 + 4х2
Определим координаты точек А и В, решив системы уравнений тех прямых, точками пересечения которых они являются.
А: 
A (2; 3);
В: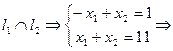 
В (5; 6).
Вычислим наименьшее и наибольшее значения целевой функции:
fmin (A)= 2·2+4·3=16,
fmax (B)= 2·5+4·6=34.