Задание 6

Выполнение этого задания требует составления модели поведения потребителей.

Типовой пример:

Пусть функция полезности потребителей на множестве двух товаров выражается целевой функцией полезности вида:

.

Цена первого товара 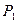= 43, второго = 59, уровень дохода D = 1200. Найти численное значение функции полезности.

Решение:

Функция полезности это отношение между объёмами потребляемых товаров и уровнем удовлетворённости потребителя.

Строим бюджетное ограничение, которое указывает, что доход потребителя должен быть равен расходам по приобретению товаров:

.

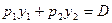Подставляем значения, заданные по условию задачи:

.

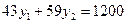Рассчитаем предельные полезности: 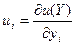, которые показывают прирост полезности при потреблении дополнительной единицы товара.

Для первого товара (i=1) u₁ = _,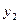

для второго товара (i=2) u₂ = _.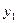

Необходимое условие оптимальности вектора У представляется условием Куна-Таккера:

,

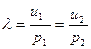подставляем все известные данные и получаем:

.

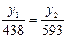Решим данное уравнение вместе с бюджетным ограничением. Получим систему линейных уравнений:

.

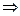
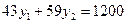Отсюда 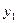= 9, 69, 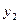= 13, 28 – оптимальные размеры покупок двух товаров при заданном уровне дохода.

Находим численное значение функции полезности:

.

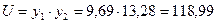Определить сколько следует выделить средств на приобретение первого ресурса, сколько на приобретение второго. Таким образом, для покупки первого товара следует выделить:

.

А для покупки второго товара следует выделить:

.

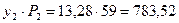Таким образом, найдены оптимальные размеры двух видов товаров, при покупке которых потребитель получит максимальную полезность и удовлетворение.

ТАБЛИЦА ВЫБОРА ВАРИАНТА