
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ЗАДАНИЕ 3. Выполнение этого задания требует знания алгоритма решения транспортной задачи.
|
|
Выполнение этого задания требует знания алгоритма решения транспортной задачи.
Типовой пример:
У поставщиков А1, А2, А3 имеется груз в количествах 300, 150 и 250 единиц соответственно, который нужно перевезти пяти покупателям: 170 ед. потребителю В1, 100 ед. – В2, 110 ед. – В3, 120 ед. – В4, и 200 ед – В5. Стоимость перевозки единицы товара от i- того поставщика j- тому покупателю задана в матрице:
С= 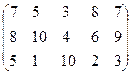
Требуется составить такой план перевозок, при котором затраты минимальны.
Решение:
Занесем данные задачи в таблицу 4 и составим первый опорный план методом наименьшего тарифа.
Таблица 4
| Потребитель Поставщик | В1 β 1=7 | В2 β 2=5 | В3 β 3=3 | В4 β 4=6 | В5 β 5=7 | Запасы | |||||
| А1 α 1=0 |
  – –
|
 + +
| |||||||||
| А2 α 2=2 |
 + +
| - | |||||||||
| А3 α 3=-4 | |||||||||||
| Потребности |
Сумма поставок по строке должна равняться соответствующим запасам, а по столбцу – потребностям; число заполненных клеток – семи.
При составленном плане вычисляем затраты:
f =170·7 + 110·3 + 20·7 + 150·9 + 100·1 + 120·2 + 30·3=3440 ден. ед.
Проверяем план на оптимальность:
1) Для заполненных клеток: α i +β i = Cij,
где
α i – потенциал поставщиков;
β i – потенциал покупателей;
Cij – тариф.
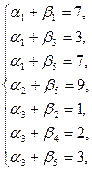
| полагая α 1 = 0, получим: β 1=7, α 2=2, β 2=5, α 3=-4. β 3=3, β 4=6, β 5=7, |
2) Проверим для свободных клеток выполнение условия оптимальности решения: α i +β i 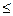 Cij, где Cij – тариф. Это условие должно выполняться во всех пустых клетках.
Cij, где Cij – тариф. Это условие должно выполняться во всех пустых клетках.
α 1+β 2=0+5=5=5, (+)
α 1+β 4=0+6=6< 8, (+)
α 2+β 1=2+7=9> 8, (не выполняется)
α 2+β 2=2+5=7< 10, (+)
α 2+β 3=2+3=5> 4, (не выполняется)
α 2+β 4=2+6=8> 6, (не выполняется)
α 3+β 1=-4+7=3< 5, (+)
α 3+β 3=-4+3=-1< 10, (+)
Условие оптимальности не выполняется для клеток (2, 1), (2, 3), (2, 4), значит стоимость перевозок может быть уменьшена.
Составим цикл пересчета для клетки (2, 1). Он проходит через клетки (1, 1), (1, 5), (2, 1), (2, 5) таблицы 1.
Перемещая по циклу поставку ρ = min (170, 150) = 150, переходим к новому плану (табл. 5):
Таблица 5
| Потребитель Поставщик | В1 β 1=7 | В2 β 2=5 | В3 β 3=3 | В4 β 4=6 | В5 β 5=7 | Запасы | |||||
| А1 α 1=0 |
  + +
|
 – –
| |||||||||
| А2 α 2=1 |
 – –
|  +
+
| |||||||||
| А3 α 3=- 4 |  – –
| + | |||||||||
| Потребности |
Затраты на перевозку при полученном плане:
f 2 = 20·7 + 110·3 + 170·7 + 150·8 + 100·1 + 120·2 + 30·3=3290 ден.ед.
Проверяем план на оптимальность:
1) Для заполненных клеток:
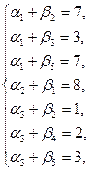
| α 1=0, α 2=1, α 3=-4, | β 1=7, β 2=5, β 3=3, β 4=6, β 5=7. |
2) Для свободных клеток:
α 1+β 2=0+5=5, (+)
α 1+β 4=0+6< 8, (+)
α 2+β 2=1+5< 10, (+)
α 2+β 3=1+3=4, (+)
α 2+β 4=1+6> 6, (не выполняется)
α 3+β 1=-4+7< 5, (+)
α 3+β 3=-4+3< 10, (+)
Условие оптимальности не выполняется в клетке (2, 4), следовательно, составленный план не является оптимальным.
Перейдем к третьему плану, составив цикл пересчета для клетки (2, 4) Он проходит через клетки (2, 1), (1, 1), (1, 5), (3, 5), (3, 4) таблицы 5.
Будем перемещать по циклу поставку ρ = min (150, 170, 120) =120. Новый план перевозок представлен в таблице 6:
Таблица 6
| Потребитель Поставщик | В1 β 1=7 | В2 β 2 =5 | В3 β 3=3 | В4 β 4=5 | В5 β 5=7 | Запасы | |||||
| А1 α 1=0 | |||||||||||
| А2 α 2=1 | |||||||||||
| А3 α 3= – 4 | |||||||||||
| Потребности |
Стоимость перевозок:
f3 = 140·7 + 110·3 + 50·7 + 30·8 + 120·6 + 100·1 + 150·3=3170 (ден.ед).
Проверка на оптимальность:
1) Для заполненных клеток:
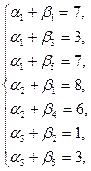
| α 1=0, α 2=1, α 3=-4, | β 1=7, β 2=5, β 3=3, β 4=5, β 5=7. |
2) Для свободных клеток:
α 1+β 2=0+5=5, (+)
α 1+β 4=0+5< 8, (+)
α 2+β 2=1+5< 10, (+)
α 2+β 3=1+3< 4, (+)
α 2+β 5=1+7< 9, (+)
α 3+β 3=-4+3< 10, (+)
α 3+β 4=-4+5< 2, (+)
Таким образом, во всех пустых клетках выполняется условие оптимальности, а значит план является оптимальным и наименьшие затраты на перевозку составляют 3170 ден. единиц.