Задания 61-70

Даны функция 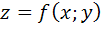, точка 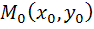и вектор 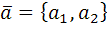. Найти:

1) градиент функции 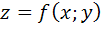в точке ;

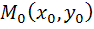2) производную функции 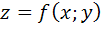в точке 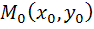по направлению вектора .

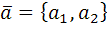61.

62.

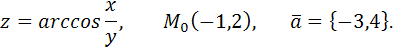
63.

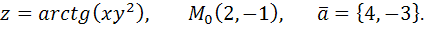
64.

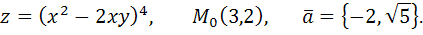
65.

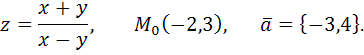
66.

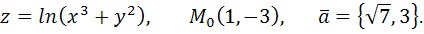
67.

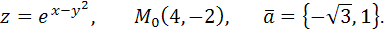
68.

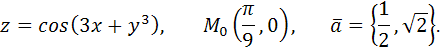
69.

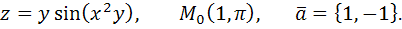
70.

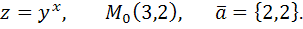
Задания 71-80

Найти:

1) частное решение дифференциального уравнения первого порядка, удовлетворяющее начальным условиям .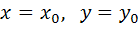

2) общее решение дифференциального уравнения второго порядка с постоянными коэффициентами.

71.

1)

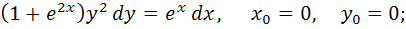
2)

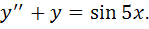
72.

1)

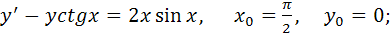
2)

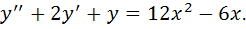
73.

1)

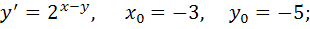
2)

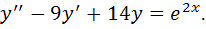
75.

1)

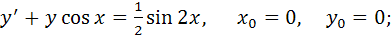
2)

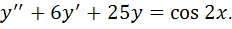
76.

1)

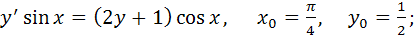
2)

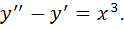
77.

1)

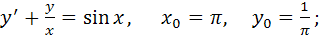
2)

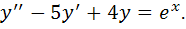
78.

1)

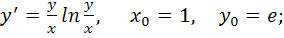
2)

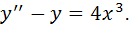
79.

1)

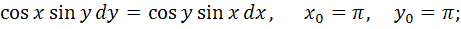
2)

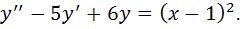
80.

1)

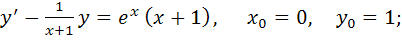
2)

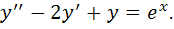
Задания 81-90

Исследовать сходимость ряда.

81.

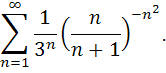
82.

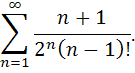
83.

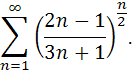
84.

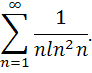
85.

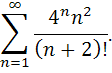
86.

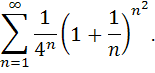
87.

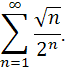
88.

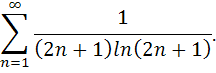
89.

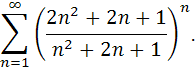
90.

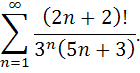
ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАНИЙ

Вычислить предел функции, не пользуясь правилом Лопиталя.

а) Если при вычислении предела получена неопределенность вида 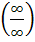, то для ее раскрытия нужно и числитель и знаменатель дроби разделить на наибольшую, входящую в них степень аргумента:

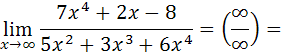
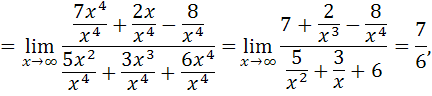
так как

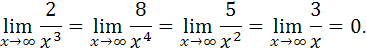
Б)

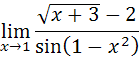
В данном случае при 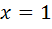и числитель, и знаменатель дроби обращаются в 0, то есть получается неопределенность вида 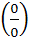. Для раскрытия неопределенности избавимся от иррациональности, умножив и числитель и знаменатель дроби на сопряженное выражение, а также воспользуемся первым замечательным пределом:

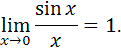
Получим:

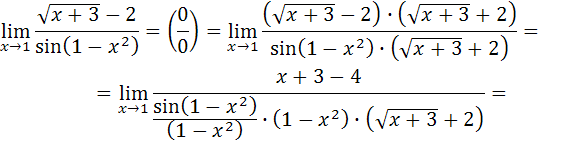
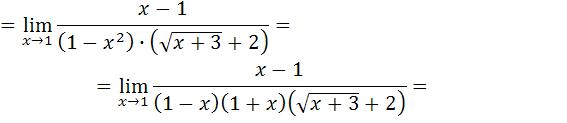
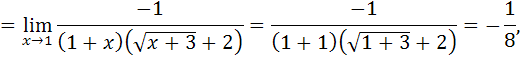
так как

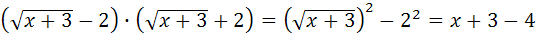
и

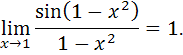
В)

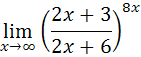
При 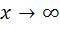получаем неопределенность вида , раскрыть которую можно воспользовавшись вторым замечательным пределом:

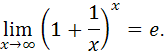
Выделяя структуру второго замечательного предела, получим:

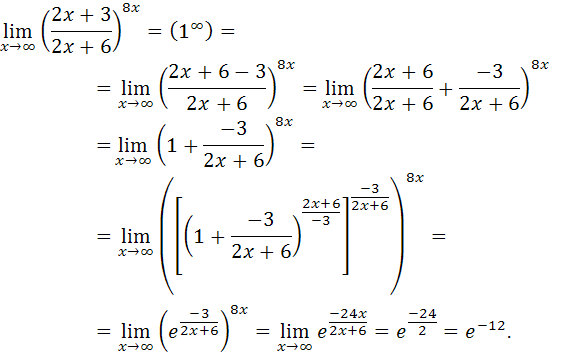
2. Найти точки разрыва функции и указать их характер.

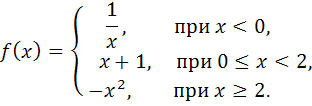
Функция определена на всей числовой оси, т.е. ,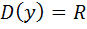

поэтому разрыв возможен только в точках 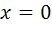и .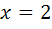

1) Пусть 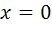. Тогда:

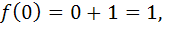
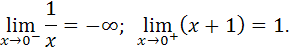
Предел функции в точке 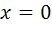слева равен бесконечности и, следовательно, точка 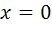является точкой разрыва второго рода.

2) Пусть 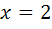. Тогда:

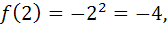
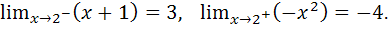
Односторонние пределы функции в точке 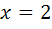конечны, но не равны. Следовательно, точка 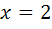является точкой разрыва первого рода, а именно точкой скачка функции.

3. Полное исследование функции проводится по следующей схеме:

1) область определения, область значений функции;

2) четность, нечетность функции, периодичность;

3) асимптоты;

4) промежутки монотонности и точки экстремума;

5) промежутки выпуклости и вогнутости графика функции, точки перегиба;

6) точки пересечения графика функции с осями координат;

7) построение графика.

Например:

а) найти асимптоты графика функции .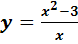

Решение.

1) Функция 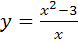не определена в точке 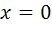. Найдем односторонние пределы функции в этой точке:

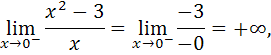
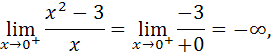
значит, прямая 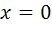является вертикальной асимптотой.

2) Найдем

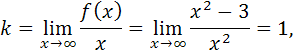
значит, функция имеет наклонную асимптоту 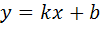, где

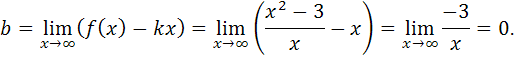
Таким образом, наклонной асимптотой графика функции 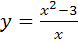является прямая .

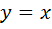б) Найти промежутки монотонности и точки экстремума функции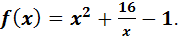

Решение.

1) Найдем производную:

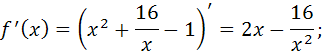
2) определим точки, в которых выполняется необходимое условие экстремума, решив уравнение :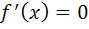

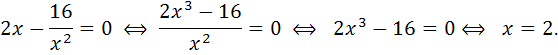
При 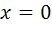производная не существует.

Точк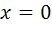и и 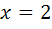разбивают числовую ось на интервалы 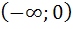, 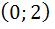и .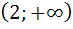

3) Определим знак производной на полученных промежутках:

Промежуток
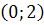
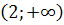
Производная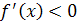

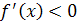
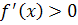
Таким образом, при 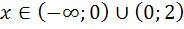функция убывает, а при 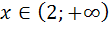− возрастает. Точка 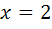является точкой минимума функции. При этом минимальное значение функции равно

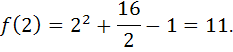
в) Найти промежутки выпуклости (вогнутости) и точки перегиба графика функции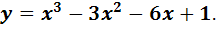

Решение.

1) Найдем производную второго порядка:

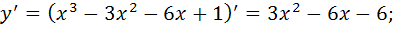
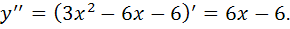
2) Найдем точки, в которых выполняется необходимое условие перегиба, решив уравнение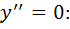

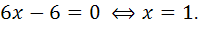
Точка 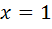разбивает числовую ось на два интервала: 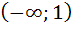и .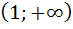

3) Определим знак второй производной на полученных промежутках:

Промежуток		.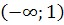
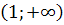Производная второго порядка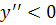

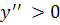
Таким образом, при 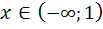график функции выпуклый вверх, а при 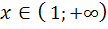− выпуклый вниз (вогнутый).

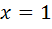− точка перегиба, в которой значение функции равно