Найти неопределенные интегралы. Результат проверить дифференцированием.

А)

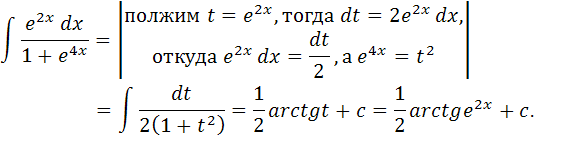
Проверка:

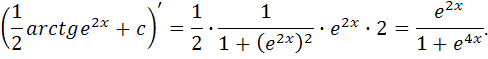
В результате дифференцирования получена подынтегральная функция, значит, интеграл найден верно.

б)

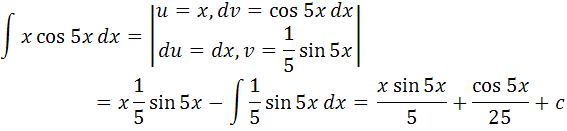
При интегрировании применялась формула интегрирования по частям: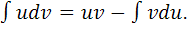

Проверка:

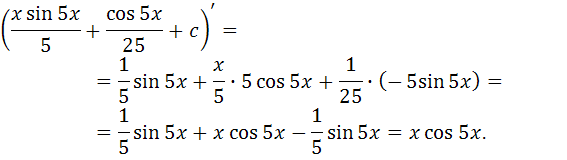
В результате дифференцирования получена подынтегральная функция, значит, интеграл найден верно.

в)

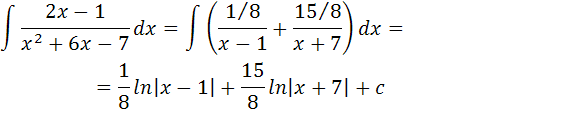
Для отыскания интеграла применяется метод неопределенных коэффициентов, согласно которому

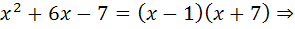
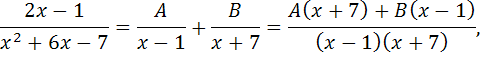
и из полученного равенства следует:

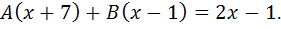
Полагая 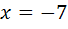, получим: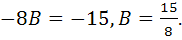

Аналогично, при 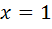получаем: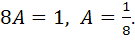

И поэтому,

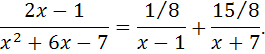
Проверка:

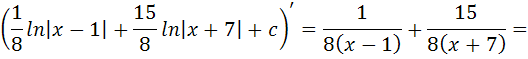
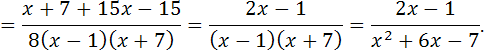
В результате дифференцирования получена подынтегральная функция, значит, интеграл найден верно.

5. Найти градиент функции 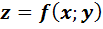в точке 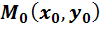, и производную по направлению вектора .

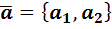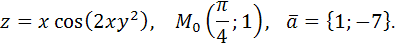
1) Найдем частные производные функции и вычислим их значения в точке .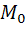

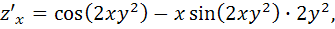
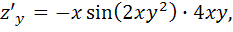
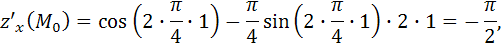
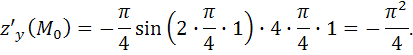
Учитывая, что 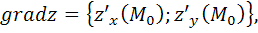получим

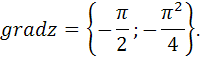
2) Найдем направляющие косинусы. Так как 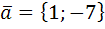, то

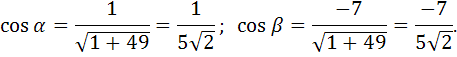
Производная функции по направлению вектор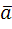а равна