
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Универсальное множество. Дополнение множества.
|
|
При решении конкретной задачи обычно встречаются множества, состоящие из элементов определенной природы. Например, в геометрии это множества точек или прямых, в арифметике- множества чисел, в социологии- множества людей и т.п. Поэтому элементы другой природы рассматривать вовсе и не требуется.
Определение 1: универсальное множество (обозначать будем U) есть множество всех рассматриваемых в данной задаче элементов.
Поскольку практически всегда ясно, с объектами какого рода мы работаем, будем считать, что все рассматриваемые ниже множества содержатся в одном и том же универсальном множестве. Таким образом, для всякого рассматриваемого множества А A_ U. Cледовательно, выполняется соотношение
A _ U = U; A _ U = A (1)
Определение 2: множество U \ А называется дополнением множества А и обозначается через А’(или АС или СА).
Формально А’={x| x_A}. Тогда A” означает (A’)’= U \ A’.
Нетрудно видеть, что
A _ A’ = U; A _ A’ = _ (2)
Утверждение 1 (закон инволюции): Для любого множества А
A” = A (3)
Доказательство:
И левая часть, и правая часть – это те и только те элементы U, которые не принадлежат А’.
Утверждение 2: Если А _ В, то В’ _ A’.
Доказательство:
Пусть x_B’. x_B. x_A. x_A’. Что и требовалось доказать.
Утверждение 3(законы де Моргана для множеств):
(A È B)’ = A’ _ B’ (5)
(A _ B)’ = A’ È B’ (6)
Доказательство:
Докажем сначала (5). x_(A _ B)’, следовательно x_ A _ B, но это равносильно истинности высказывания 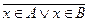 T
T 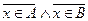 , что означает, что истинно x_A) x_B, то есть x_A’) x_B’, а значит x_A’_B’.
, что означает, что истинно x_A) x_B, то есть x_A’) x_B’, а значит x_A’_B’.
Докажем (6), используя (5): (A’_ B’)’ = A”_ B” = A _ B, отсюда (A_B)’ = (A’_B’)”. (A _ B)’ = A’_B’. Что и требовалось доказать.
|
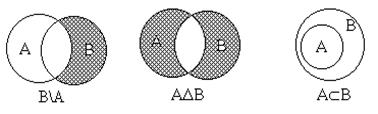
Многие свойства множеств удобно иллюстрировать при помощи диаграмм Эйлера-Венна. При этом удобно множество изображать кругами или другими связными фигурами. U- прямоугольником, внутри него остальные множества.
Например, легко увидеть(нарисуйте), что (A_B) \B=А не всегда верно, а если А_B=_, то верно.
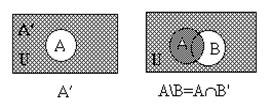 Поэтому удобно, прежде чем доказывать какое-либо теоретико-множественное равенство, представить его левую часть и правую часть при помощи диаграмм Венна.
Поэтому удобно, прежде чем доказывать какое-либо теоретико-множественное равенство, представить его левую часть и правую часть при помощи диаграмм Венна.
И в заключении параграфа введем еще одно важное понятие, связанное с количеством элементов множества.
Рассмотрим множество А={1; 2;...; n}={x| x_ N) 1_x_n}. Оно содержит n элементов. Будем говорить, что мощность множества А есть n и записывать: |A|=card(A)=n.
Далее будем говорить, что любое множество В, имеющее то же число элементов, что и А, имеет мощность n.
Определение 3: говорят, что множество Х конечно, если Х=Æ или если существует число n_ N, такое, что Х имеет такое же число элементов, что и {1; 2;...; n}, то есть /Х/=n. Если Х _ Æ и такого n не существует, то Х называют бесконечным.
Пример: 1) A={x| x_ Z) -2_x< 2}|A|=4
2) В классе 30 человек, они изучают французский и английский языки. Французский изучают 12 человек, английский— 25. Сколько человек изучают оба языка? (ответ 7 человек)
3) Доказать формулу: |A_B| = |A|+|B|+|A_B|, если A и B конечные множества.