
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Глава III
|
|
Отношения
В этой главе мы рассмотрим понятия отношения между элементами данного множества и между элементами нескольких множеств. Это интуитивно ясное понятие (например, элементы двух множеств находятся в некотором отношении, если они удовлетворяют некоторым требованиям) является довольно общим. Поэтому оно широко применимо. Приведем несколько описательных примеров.
Два элемента из множества всех людей могут находиться в отношении «быть родственниками»; два слова из словаря могут находиться в отношении «порядка следования по алфавиту»; элементы из множества всех треугольников могут находиться в отношении «иметь равную площадь»; два элемента из множества N могут находиться в отношении «быть делителем» и т.п.
Прежде чем подойти к этому вопросу с математической позиции, рассмотрим несколько идей, возникающих из рассмотрения следующей простой ситуации. Предположим, что для некоторой машины мы имеем конечное множество программ Р, конечное множество значений данных Д и множество результатов R. Каждый элемент из Д может использоваться в некоторых программах из Р и каждый элемент из Р может использовать некоторые данные из Д. Если d_Д и р_Р, то d и р могут находиться в отношении «возможность использования». Поэтому имеет смысл рассматривать пары (d, p) так, что р может использовать d. Но множество таких пар есть подмножество D‘P. Если, например, мы рассмотрим некоторую программу р_Р, то она связывает некоторые элементы из Д с результатами из R. Тогда имеет смысл изучать некоторое подмножество Д‘R‘P таких элементов (d, p, r), что результат r получен из d при помощи программы р. Это уже отношение между элементами трех множеств.
Теперь можно переходить к формальным рассмотрениям:
Основные понятия
Определение 1: n-местным отношением R на множествах А1, A2, …, An называется подмножество прямого произведения A1‘A2‘…‘ An. Другими словами, элементы x1, x2,..., xn связаны отношением R тогда и только тогда, когда (x1, x2,..., xn)_R_ A1‘A2‘…‘ An.
Наиболее часто встречаются отношения при n=2. В этом случае они называются бинарными отношениями. Таким образом, бинарное отношение на множествах А и В есть просто подмножество А‘В. Если же А=В, то это подмножество А2. В этом случае будем говорить, что отношение задано на множестве А. В основном мы будем изучать бинарные отношения.
Пример:
Пусть А={1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Зададим R на А: R={(x, y)| x, y_A) x делитель y) x_5}. Его можно выписать в явном виде: R={(1, 1), (1, 2),..., (1, 10), (2, 2), (2, 4), (2, 6), (2, 8), (2, 10), (3, 3), (3, 6), (3, 9), (4, 4), (4, 8), (5, 5), (5, 10)}.
В общем случае количество различных отношений на множестве А зависит от |A|. Большая часть этих отношений не представляет особого интереса. Ниже дадим определение трех отношений, которые имеют важное значение при построении теории бинарных отношений.
Определение 2: Пусть А - произвольное непустое множество. Отношение IA={(a, a)| a_A} называется тождественным отношением на А. Отношение UA={(a, b)| a_A) b_A} называется универсальным отношением на А, то есть UA=A2. Кроме того, Æ _ А2, значит оно тоже является(определяет) отношением на А и называется пустым отношением.
Пусть R - бинарное отношение на множествах А и В. Поскольку R всего лишь подмножество А‘В, то может случиться так, что не все а_А и b_B находятся в отношении R.поэтому имеет смысл ввести следующие понятия:
Определение 3: Областью определения D( R ) бинарного отношения R_A‘B называется такое подмножество А, что D(R)={x| (x, y)_R}. Областью значений E( R ) бинарного отношения называется такое подмножество В, что E(R)={y|(x, y)_R}. Если R_A2, то D(R)_A и E(R)_A.
Пример: Если R есть отношение из предыдущего примера, то D(R)={1, 2, 3, 4, 5}, E(R)=A.
Существует три основных способа записи того, что элементы а и b находятся в некотором отношении. С одним из них мы уже встречались:
1. (a, b)_R. Другой способ использует строчные греческие буквы:
2. a R b, «а связано с b отношением R», то есть высказывание a R b истинно. Это удобно, когда для конкретного отношения существуют специальный символ. Например, r_N2 и r={(x, y): x< y}, здесь вместо 6 r 7 можно писать 6< 7.
3.b_R (a) это функциональная запись отношения.
Из заданного бинарного отношения можно построить другие отношения, например обратное к R.
Определение 4: Пусть R — бинарное отношение. Обратным (инверсным) к R отношением называется следующее отношение: R-1={(x, y)| (y, x)_R}.
Следовательно, если R _ A‘B, то R-1 _ B‘A. Тогда из определения получаем, что D(R-1)=E(R) и E(R-1)=D(R).
В дальнейшем будем обозначать D(R)=DR, E(R)=ER.
Пример: Пусть X={2, 4, 6, 8}, r={(x, y)| x, y_X) x< y}. Выпишем r и r-1:
r={(2, 4), (2, 6), (2, 8), (4, 6), (4, 8), (6, 8)}, Dr={2, 4, 6}, Er={4, 6, 8},
r-1={(4, 2), (6, 2), (8, 2), (6, 4), (8, 4), (8, 6)}.
В заключение этого параграфа рассмотрим некоторые методы графического изображения отношений, заданных на «небольших» множествах. Поскольку, при решении конкретной задачи, особенно на первом этапе, рисунок может оказаться весьма полезным.
Пусть X={a, b, c, d, e}. Рассмотрим отношения IX, UX и R={(a, b), (a, c), (b, d), (c, e), (e, b)}.
На координатной плоскости: 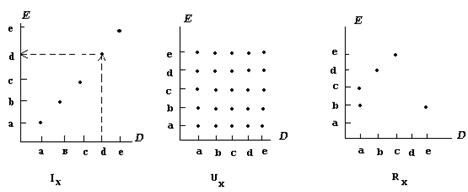
Одним из наиболее часто встречающихся методов изображения отношений является изображение с помощью графа:
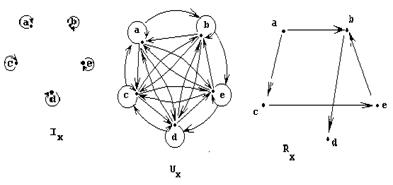
Это изображение более наглядно и для изучения свойств небольших отношений является достаточно эффективным.