Отношение порядка.

Из понятия равенства (например, чисел) возникает математическое понятие эквивалентности. А из понятия неравенства возникает другой тип отношений, которые называются отношениями порядка.

Определение 1: Частичным порядком на множестве А называется бинарное отношение, которое рефлексивно, антисимметрично и транзитивно.

Частичный порядок - это обобщение отношения £ на R. Можно ввести понятие строгого порядка, соответствующего отношению < на R. Отношение строгого порядка - только транзитивно(оно еще и антирефлексивно).

Если задан £, то можно определить <: a< b Û a£ b Ù a¹ b. Если задан <, то можно определить £: a£ b Û a< b Ú a=b.

Множество, на котором задано отношение порядка, будем обозначать

(X, £) (или (X, <), если порядок строгий).

Определение 2: Множество, на котором задано отношение порядка, называется частично упорядоченным.

Пример: A - множество. (P (A), Í), легко проверить, что отношение Í является отношением порядка на P (A).

Определение 3: Отношение порядка R на А называется полным ( линейным ) порядком, если " x, yÎ A (xR y Ú yR x). Множество (A, R) называется линейно упорядоченным.

Примеры:

1. отношение £ на R является отношением полного порядка. Таким образом (R, £) - линейно упорядочено.

2. а вот (P (A), Í) не является линейно упорядоченным

3. x£ y Û y 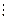x на множестве N не является полным порядком

Определение 4: пусть (A, £) – частично упорядоченное множество. Элемент аÎ А называется наименьшим /наибольшим/ в А, если " xÎ A (a£ x) /x £ a /. Элемент bÎ А называется минимальным /максимальным/ если " xÎ A (x£ a Þ x=a) /a £ x Þ a=x /.

Задача: Доказать, что для линейно упорядоченного множества понятия наибольшего (наименьшего) и максимального (минимального) элементов совпадают. Привести пример частично упорядоченного множества, где они не совпадают.