Замыкание отношений

Понятие замыкания является фундаментальным математическим понятием и используется в большинстве разделов математики. Проиллюстрируем это понятие на общем примере: возьмем объект x₀ и процесс P, который, будучи примененный последовательно, порождает некоторое множество и, значит, определяет последовательность x₁, x₂,..., x_n,... так, что x₁Î P(x₀), x₂Î P(x₁),..., x_nÎ P(x_n-1),...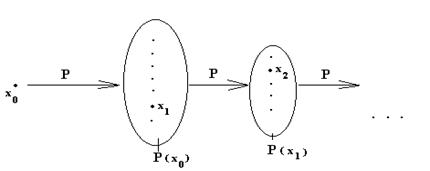

Определение 1: множество, содержащее все элементы всех последовательностей, которые могут быть получены при помощи процесса P и начинающиеся с x₀, называется замыканием процесса P относительно x₀.

Ясно, что результат будет заключаться в нахождении Рⁿ(x₀) при некотором n. Это n мы заранее не знаем, оно зависит от самого процесса. Более того, если мы возьмем элемент y из этого замыкания и будем применять к нему процесс р, то не получим ничего нового. То есть множество таким путем расширено быть не может - оно замкнуто!

Пример: Возьмем квадрат S, обозначенный ABCD и рассмотрим процесс r, заключающийся в повороте квадрата по часовой стрелке на 90°:

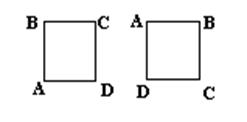
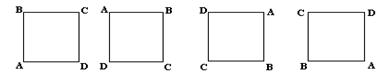
Пусть отношение A задано на некотором множестве. Тогда:

Определение 2: Транзитивным замыканием отношения A на данном множестве называется отношение A⁺:

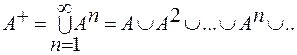
Таким образом, из не транзитивного отношения A на некотором множестве можно построить транзитивное A⁺.

Примеры:

1. r - отношение на N: r={(x, y)| y=x+1}, тогда r⁺={(x, y)| x< y}

2. s на Q: s={(x, y)| x< y}, тогда s⁺=s

3. t на Q: t={(x, y)| x× y=1}, тогда r⁺={(x, x)| x¹ 0}

4. Пусть L - множество станций лондонского метро; L={a, b, c} последовательные станции. N={(x, y)| y следует за x}.Значит (a, b), (b, c) Î N; кроме того (a, a), (b, b), (c, c), (a, c) Î N². Значит, N⁺=L´ L

Вообще говоря, транзитивное замыкание не является рефлексивным (пример 2).

Пусть A - отношение на X. Положим A⁰=I_X.

Определение 3: Рефлексивным замыканием А* отношения A называют отношение . То есть .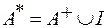

Примеры:

1. r*={(x, y)| x£ y}

2. s*={(x, y)| x£ y}

3. t* = t⁺È {(0, 0)}

4. N*=N⁺