
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определения и основные свойства.
|
|
Определение 1: Бинарное отношение r между множествами A и B(rÌ A´ B) называется функцией, если arbÙ arc Þ b= c. То есть если " xÎ A существует не более одного элемента yÎ B такого, что xry.
Если xry, то нам удобно будет записывать y=r(x), при этом первый элемент пары (x, y) будем называть аргументом, а второй- значением функции на элементе x, или просто функция от x.
Функции обычно обозначаются строчными буквами латинского алфавита f, g, h,... или специальными наборами символов, таких как sin, log,...
Говорят, что функция f действует из A в B и записывают это так: f: A®B, если при этом x f y, то есть y=f(x), то говорят, что функция f отображает элемент x в y и записывают так: f: x ay. Или говорят, что y есть образ элемента x при отображении f, а x есть прообраз y. Последнее обозначение удобно, когда следует явно указать закон, по которому действует функция.
Пример 1: f: A®A, где A={-1; 0; 1} по правилу f: x ax3.
Пример 2: Это пример того, что не всякое отношение является функцией
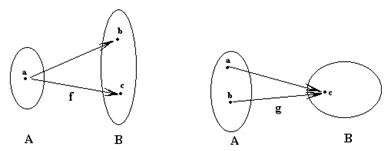
а) f - не является функцией б) g - является функцией
Поскольку всякая функция, действующая из A в B, является отношением на множествах A и B, то можно дать следующее определение:
Определение 2: Областью определения функции f: A®B называется область определения отношения fÌ A´ B, то есть Df={xÎ A| $yÎ B ((x, y)Î f)}={xÎ A| $yÎ B (x f y)}={ xÎ A| $yÎ B (y=f(x))}, то есть DfÍ A.
Определение 3: Областью значений функции f: A®B называется область значений отношения fÌ A´ B, то есть Ef={yÎ B| $xÎ A ((x, y) Î f)}= {yÎ B| $xÎ A (x f y)}= {yÎ B| $xÎ A (y=f(x))}, то есть EfÍ B.
Определение 4: Две функции f: A®B и g: A®B называют равными и пишут f=g тогда и только тогда, когда они равны как подмножества прямого произведения A´ B, то есть если (x, y)Î f Û (x, y)Î g.
Замечание: Ясно, что если f=g, то Df=Dg и Ef=Eg.
Вопрос: Верно ли обратное утверждение? Если нет, то приведите пример.
Определение 5: Функция f: A®B называется отображением, если ее область определения совпадает с A (Df=A). При этом говорят, что f отображает множество A в (или на) множество B.
Примеры:
3. sin: R ® R, отображение множества R в R
4. ln: R ® R – функция, действующая из R в R. Dln={xÎ R | x> 0}= R +. ln: R +® R – здесь уже является отображением множества R + на все R.
Определение 6: Функция f: A® R называется функцией, принимающей действительные значения. Функцию f: R ® R называют действительной (вещественной) функцией.
Определение 7: Если f: A®B и A есть прямое произведение множеств A1´ A2´...´ An, то говорят, что f есть функция n переменных. Тогда вместо f((x1, x2,..., xn))пишут f(x1, x2,..., xn).
В частности: f(x, y) - функция двух переменных, f(x, y, z) - функция трех переменных.
Примеры:
5. f: R ´ R ® R. f(x, y) a x+y, то есть (x, y, x+y)Î fÌ R 3. В этом случае можно писать z=x+y.
6. f: N ´ N ® Q. f(x, y) a x/y, можно записать z=x/y
В математике часто используются функции и отображения, которые обладают некоторыми очень важными свойствами.
Определение 8: Функция f: A®B называется сюръективной («на», то есть действует из A на B) если Ef=B. Или: 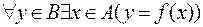 .
.
Другими словами: у каждого элемента из B есть прообраз в A.
Определение 9: Функция f: A®B называется инъективной, если 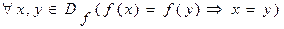 .
.
Условие инъективности можно записать следующим образом: " x, yÎ Df(x¹ yÞ f(x)¹ f(y)) (почему?)
Определение 10: Функция f: A®B называется биективной, если она инъективна и сюръективна.Если Df=A, то говорят, что f - биекция или взаимно-однозначное отображение множества A на множество B.
Примеры:
7. отображение из примера 2 б) сюръективно, но не инъективно
8. sin: R ®[-1; 1] сюръективно, но не инъективно, а вот sin: [-p/2; p/2]®[-1; 1] – биекция
9. exp: R ® R. exp: x a ex инъективно, но не сюръективно
10. f: N ®{натуральные, четные}; f: n a 2n - биекция