
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Отношение эквивалентности.
|
|
Во многих вычислительных задачах берутся большие множества и разбиваются таким образом, чтобы все интересующие нас ситуации можно было исследовать на нескольких правильно выбранных примерах.
Определение 1: Пусть A ¹ Æ и {Ai}, i= 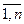 совокупность подмножеств таких, что A=
совокупность подмножеств таких, что A= 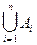 . Тогда совокупность этих подмножеств называется покрытием множества A.
. Тогда совокупность этих подмножеств называется покрытием множества A.
Например, {A, B}- покрытие AÈ B; {A, AÈ B, B, C}-покрытие AÈ BÈ C.
Замечание: В общем случае покрытие может быть и бесконечным. однако с точки зрения изучения конкретных свойств такая ситуация не вызывает энтузиазма.
Определение 2: Разбиением непустого множества А называется такое его покрытие 
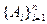
 , что если i¹ j, то AiÇ Aj=Æ.
, что если i¹ j, то AiÇ Aj=Æ.
Например, {A, A’} – разбиение U.
{AÇ B, AÇ B’, A’Ç B, A’Ç B’} – разбиение U,
{A\B, AÇ B, B\A} – разбиение AÈ B.
Организовать разбиение непустого множества можно при помощи отношений, которые ведут себя подобно отношениям равенства на множестве чисел или множеств.
Определение 3: Бинарное отношение на множестве называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.
Примеры:
1. На множестве всех треугольников: {(x, y)| x и y имеют одинаковую площадь}
2. На множестве всех программ: {(a, b)| a, b вычисляют одну и ту же функцию на конкретной машине}
Определение 4: Пусть R – отношение эквивалентности на множестве А и xÎ A. Классом эквивалентности порожденным элементом х называется множество {y| xR y}=[x]R.
Определение 5: Любой элемент класса эквивалентности называется представителем этого класса. Полной системой представителей называется множество представителей, по одному из каждого класса.
Пример 3:
N – натуральные числа, s – фиксированный элемент. На Z определено отношение: rs= {(x, y)| x-y=ns, nÎ Z }. Отношение сравнения по модулю s (запись: xº y(mod s)).
Нетрудно проверить, что отношение сравнения по модулю s, есть отношение эквивалентности на множестве Z.
Пусть, например, s=10. Тогда:
[1] = {11, 21, -9, 10 976 631,.... }
[1066] = {66, 226, -24,... }
На самом деле есть всего 10 классов эквивалентности по этому отношению, а числа 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 образуют полную систему представителей. Классы эквивалентности по этому отношению эквивалентности называют классами вычетов по модулю s.
Определение 6: Фактор-множеством множества А по отношению эквивалентности R называется множество всех классов эквивалентности по этому отношению и обозначается A/R.
Множество классов вычетов по модулю s обозначают Zs.
Имеет место
Теорема (о разбиении): Пусть R - отношение эквивалентности на непустом множестве А. Тогда фактор-множество A/R является разбиением множества А.
Доказательство:
" xÎ A(xÎ [x]R). Надо доказать, что каждый элемент множества А принадлежит в точности одному классу. То есть, докажем, что если классы имеют хотя бы один общий элемент, то они совпадают. Пусть cÎ [a] и cÎ [b]. Пусть xÎ [a], но тогда x R a, a R c, c R b Þ x R b(транзитивность R). Значит, [a] Ì [b]. (где рефлексивность? а она есть!) Аналогично [b] Ì [a].
Что и требовалось доказать.
Имеет место и обратное утверждение. Пусть S- разбиение множества А и Rs – бинарное отношение на A, такое что: R={(x, y)ï x и y принадлежат одному элементу разбиения }, тогда R, будем называть– отношением, определяемым разбиением S.
Теорема (обратная): Отношение R на А, определяемое разбиением S, является отношением эквивалентности на А, причем A/Rs=S.(самостоятельно)
Упражнения:
1. Пусть А- конечное множество. Какие отношения эквивалентности дают наибольшее и наименьшее число классов эквивалентности.
2. Если {A1, A2,..., An}- разбиение А и А конечно, то 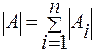 .
.