
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Композиция отношений
|
|
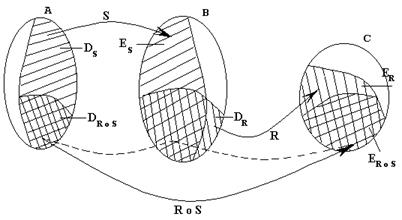
Пусть заданы множества A, B и C и отношения S между A и B (то есть SÌ A´ B) и R между B и C (RÌ B´ C). Определим новое отношение между A и C следующим образом:
Определение 1: Множество всех пар (x, y), таких, что существует zÎ B такое, что (x, z)Î S и (z, y)Î R называется композицией отношений S и R. Обозначается: R o S. Таким образом, R o S Ì A ´ C.
R oS = {(x, y)| $zÎ B((x, z)Î SÙ (z, y)Î R)} или x R o Sy Û $zÎ B(xSzÙ zRy).
Пример 1: Пусть A={1, 2, 3}, B={1, 2, 3, 4, 5, 6}, C={3, 6, 9, 12}, s ={(1, 2), (2, 4), (3, 6)}, r={(1, 3), (2, 6), (3, 9), (4, 12)}. Тогда r o s={(1, 6), (2, 12)}.
Проиллюстрируем ситуацию на картинке:
Пример 2: Пусть s и r - отношения на N такие, что
 s = {(x, x+1)ï xÎ N } и r = {(x2, x)ï xÎ N }. Тогда Dr = {x2ï xÎ N }={1, 4, 9, 16, 25,...}, а Ds= N.
s = {(x, x+1)ï xÎ N } и r = {(x2, x)ï xÎ N }. Тогда Dr = {x2ï xÎ N }={1, 4, 9, 16, 25,...}, а Ds= N.
Dros={xï xÎ N Ù x+1=y2}={3, 8, 15, 24,...}.
В случае, когда отношение задано на множестве, оно может быть скомбинировано с самим собой:
sos = s2 = {(x, x+2)½ xÎ N } и ror = r2 = {(x4, x)½ xÎ N }.
Используя это обозначение, можно определить энную степень отношения:

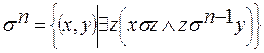 , где nÎ N, n> 1.
, где nÎ N, n> 1.
Например, для отношений из примера 2 имеем:
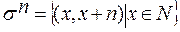 ,
, 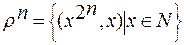
Хотелось бы дополнить аналогию с умножением. Для этого введем следующее естественное определение:
Определение 2: Бинарные отношения называются равными, если они равны как подмножества, то есть R=S, если" x, y((x, y)Î RÛ (x, y)Î S).
Понятно, что отношения должны быть определены на одних и тех же множествах.
Теорема (свойства композиции отношений): Для любых бинарных отношений R, S, T имеют место равенства:
1. (RoS)oT = Ro(SoT)
2. (RoS)-1 = S-1o R-1 
Доказательство:
1) Для любых x и y имеем:
x(RoS)oTy º $z(xTzÙ (zRoSy)) º $z$t(xTzÙ (zStÙ tRy)) º $z$t((xTzÙ zSt)Ù tRy) º $t(($z(xTzÙ zSt))Ù tRy) º $t((xSoTt)Ù tRy) º xRo(SoT)y.
2) x(RoS)-1y º yRoSx º $z(ySzÙ zRx) º $z(xR-1zÙ zS-1y) º xS-1oR-1y.
Что и требовалось доказать.
Замечание: если R - отношение на множестве A, то ясно, что IAoR=RoIA=R. То есть IA ведет себя как единица при умножении чисел. Однако полной аналогии провести нельзя. Поскольку, например, коммутативность, в общем случае места не имеет, так как RoS может быть определено, а SoR нет. Также как и не всегда имеет смысл равенство R-1oR=RoR-1= IA.