Обобщающие показатели. Средние величины.

На этапе стат. сводки от индивидуальных значений признаков совокупности, путем суммирования переходят к показателям совокупности, которые называются обобщающими.

Средние величины - обобщающая характеристика совокупности однотипных явлений по варьируемому признаку. Она показывает общее и типичное для всей совокупности в конкретных условиях.Сущность: отражении общих черт и закономерностей экон-их явлений и процессов. Средние бывают: степенные (арифметическое, геометрические, гармонические); структурные (мода, медиана).

Применение средних величин: Сред. ариф-ая простая применяется когда расчет осуществляется по несгруппированным данным; Сред. ариф-ая взвешенная - для сгруппированных данных или доп. распределений; Сред. гармон. взвешенная используется, если неизвестны частоты n_i, а известны произведения x_i*n_i; Сред. гармон. простая -все x_i*n_i равны между собой; Сред. геометр. - в анализе рядов динамики для определения средних темпов роста; Средняя квадратическая используется в расчетах показателей вариации.

8.Степенные сред. величины. Соотношение средних…..

1)средняя арифметическяя 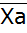= 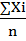– простая; 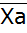= 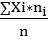– взвешен. 2)средн.квадратическая: 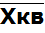= 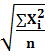- простая; 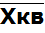= 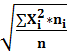– взвеш

3)средняя геометрическая: 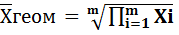- простая;

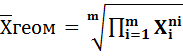– взвешенная

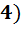средняя гармоническая 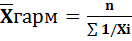-простая;

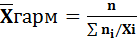– взвешенная

Правило мажорантности средних: с ростом показателей степени значения средних возрастают: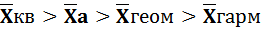

Свойства средней арифметической величины:

1.Средняя арифметическая константы = самой этой константе 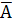=А

2.Средняя арифметическая суммы = сумме средних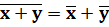

3.Если Xi увеличить или уменьшить на одно и то же число, то сред. ариф-ая увел-ся или умень-ся на это же самое число: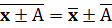

4.Если Xi увеличить или уменьшить в одно и тоже число раз, сред. ариф-ая увел-ся или умень-ся в это же число раз: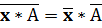

5.Если все весовые коэффициенты n_i увеличить или уменьшить в А раз, средняя арифметическая не изменится

6.Сумма отклонений значений признака от средней величины = 0

7.Сумма квадратов отклонений значений признака от средней арифметической < суммы квадратов отклонений от произвольного числа: <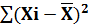

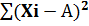
Применение средних величин: Сред. ариф-ая простая применяется когда расчет осуществляется по несгруппированным данным; Сред. ариф-ая взвешенная - для сгруппированных данных или доп. распределений; Сред. гармон. взвешенная используется, если неизвестны частоты n_i, а известны произведения x_i*n_i; Сред. гармон. простая -все x_i*n_i равны между собой; Сред. геометр. - в анализе рядов динамики для определения средних темпов роста; Средняя квадратическая используется в расчетах показателей вариации.