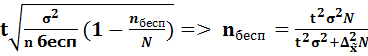Нормально распределение. Кривая. Правило трех сигм.

Распределение величины Х наз.нормальным, если плотность распределения этой величины, выражается формулой: f(x)=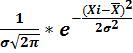

Нормал. распределение - двухпараметрическое распределение (имеет 2 параметра: сред.величина и сред. квадратическое отклонение).

f(x) Кривая

нормального

распределения

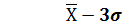
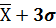
а

«Правило трех сигм» Если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднеквадратического отклонения.

|x_i - a| 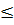3Ϭ; а - 3Ϭ 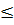Xi 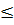а + 3Ϭ

Правило «трёх сигм» применяется, если распределение случайной величины неизвестно, но выполняется условие «трех сигм», то предполагают, что эта величина распределена нормально.

P (|x - a| 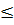Ϭ)=0, 6823; P (|x - a| 2Ϭ)=0, 9545; P (|x - a| 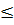3Ϭ)=0, 9973

15.Критерии согласия. Проверка гипотезы распределения…

Критерия согласия -критерий проверки гипотезы о предполагаемом законе распределения: Смирнова; Колмагорова; Критерии Пирсона:

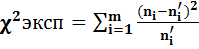
Алгоритм проверки:

1.Выдвигается гипотеза Н₀: совокупность распределена нормально

2.Вычисляются теоретические частоты и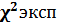

3.По таблице «критические точки распределения 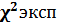» при заданном уровне значимости и числе степеней свободы, находят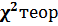

4.Если в результате сравнения 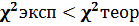, то Но не отвергается. В противном случае 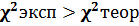- отвергается.

Ошибка 1рода состоит в том, что будет опровергнута правильная гипотеза. Эту ошибку называют уровнем значимости(альфа )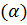

Ошибка 2рода состоит в том, что будет принята неправильная гипотеза.

Число степеней свободы: 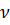= n – k – 1

16. Оценка отклонения теорет. Распределения от нормального…

Оценка отклонения теоретического распределения от нормального осуществляется с помощью показателей асимметрии(As) и эксцесса(Ek).

As= 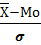, -3< As< 3; Ek= 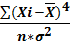– 3

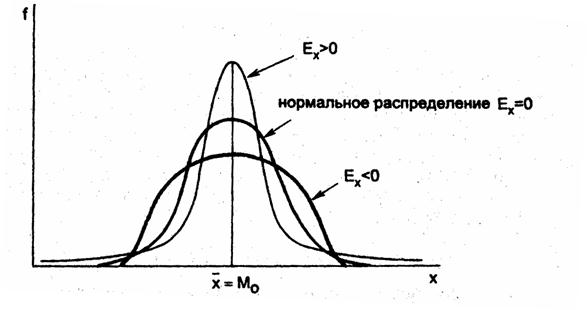
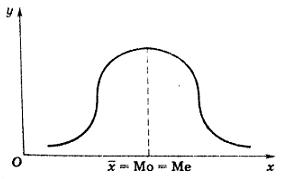
Ek=0 – распределение нормальное

Ek> 0-распределение

островершинное

Ek< 0-распределение плосковершинное
Мо< Ме< 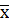- правосторонняя ассиметрия (As> 0); 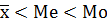- левосторонняя ассиметрия (As< 0); Ме= 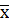- симметричное нормальное распределение (As=0).

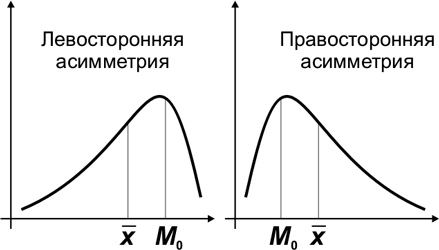
As> 0, 5 - значительна; As< 0, 25 – не значительна

17. Понятие выборочной и генеральной совокупности. Виды…

Выборочное наблюдение – вид статистического наблюдения, при котором обследованию подвергается не вся совокупность, а лишь часть её единиц, отобранных в определенном порядке, при этом вся совокупность в целом называется генеральной, а единицы подвергающиеся наблюдению называются выборочной совокупностью или выборкой.

Виды отбора: 1) повторный – отбор, при котором отобранный объект перед отбором следующего возвращается в генеральную совокупность 2)бесповторный – отбор, при котором отобранный объект, в генеральную совокупность не возвращается.

Способы отбора: 1)Отбор, не требующий расчленения генеральной совокупности на части: а) простой случайный бесповторный отбор; б) простой случайный повторный отбор.

2)Отбор, при котором генеральная совокупность разбивается на части:

а) случайный – отбор, при котором объекты извлекаются случайным образом по одному из генеральной совокупности

б) типический – отбор, при котором объекты отбираются не из всей совокупности, а из каждой её качественно-однородной группы

в) механический – отбор, при котором генеральную совокупность делят на столько групп, сколько объектов должно войти в выборку и затем из каждой группы выбирают один объект

г) серийный – отбор, при котором объекты отбирают из генеральной совокупности сериями, которые затем подвергают обследованию

18.Ошибки выборки: средняя, предельная, относительная….

Ошибки выборки: 1)Средняя:

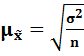– для повторного отбора; 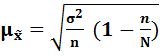- для бесповтор-го

2)Предельная: 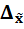= t* 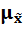, где t- коэф-т доверия, определяется по таблице значений Лапласа при заданной доверительной вероятности

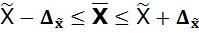, где 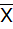-генеральная средняя; -выборочн. средняя

3)Относительная: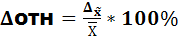

При планировании выборочного наблюдения необходимо решить задачу нахождения необходимой численности выборки(n), обеспечивающей определенную точность расчета оценок параметров генеральной совокупности, эти значения (n) можно оценить:

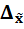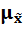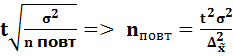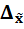= t* = ;

= t* 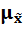=